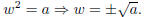Basic Algebra: Quadratic Formula
In many of your science ( and math ) classes you can often
solve a quadratic equation by using the quadratic formula. This
replaces having to go through the process of completing the square (remember,
competing the square in general is what
leads to the quadratic formula ).
You must memorize the quadratic formula.
Questions
Include complex solutions in your answers . Some of these
equations can be solved easily using techniques other than the
quadratic formula.
1. Write down the quadratic formula that solves ax^2 + bx + c = 0.
2. Solve x ^2 =2/3x.
3. Solve 7x^2 + 4x − 3 = 0.
4. Solve 4x^2 + 3x − 2 = 0.
5. Solve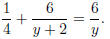 
6. Solve 2x^2 + 15 = 0.
7. Solve 5x^2 = −3.
8. Use the discriminant to find what type of solution 9x^2 + 4 = 12x has.
9. Write a quadratic equation which has the solutions 1 − 4i and 1 + 4i.
Solutions
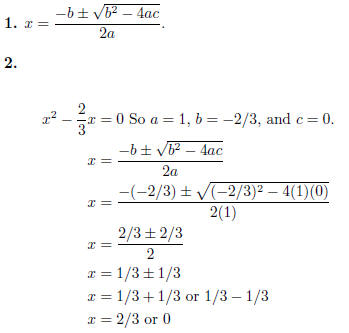
Since c = 0, this could have been solved by factoring :
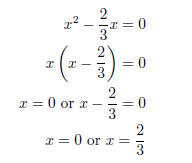
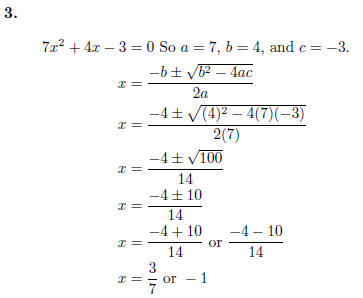
This could also have been done using factoring by grouping .
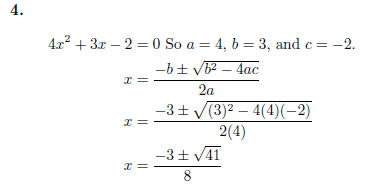
Because the roots are complicated , the only way to do this
one was using quadratic formula or completing the square.
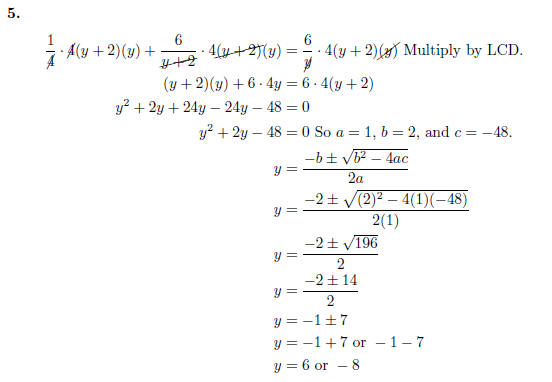
Recall than when you multiply by an LCD to solve an equation, you must check for extraneous solutions.
Check y = 6 :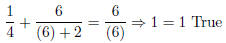
Check y = −8 :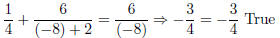
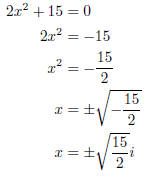
7. Solve using quadratic formula.
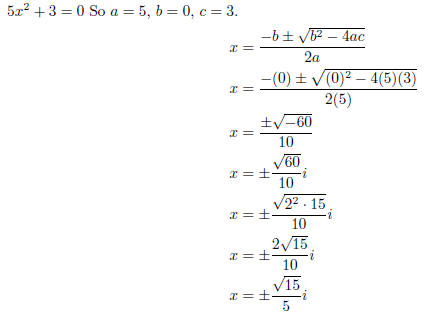
8. The discriminant is b^2 − 4ac = (−12)^2 − 4(9)(4) = 0.
This means there will be one rational root .
9. If the quadratic has solution r , then it has a factor (x − r).
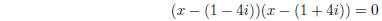Now, carefully multiply
everything out to get the quadratic.
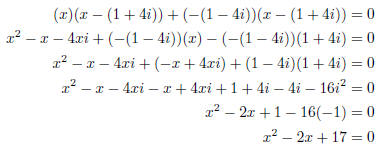
| Prev | Next |