Tutoring Notes for Exponential and Logarithmic Equations
Preliminary Comment : We spend more time in class on
these sections than on any other
material in the course. Many students haven't studied this material in high
school and they
generally find it very difficult.
Section 4.1: We will cover everything in this
section except for compound interest. We
won't spend time on how to use a calculator to evaluate exponential functions,
although
there will be some homework problems where students will need a (scientific)
calculator.
Here are some difficulties that I expect students to have have in this section:
• Students need to be reminded regularly that ax > 0 for
all values of x. In particular,
they need to be reminded that the equation a x = 0 has no solutions. Point this
out to
students often. They also occasionally forget that a0 = 1.
• The number e might be unfamiliar to many students. What we tell them in this
course
is that: e is an extremely important number, it's a special irrational number
(just like
π), its value is about 2.718, and for reasons that we can't explain in this
course, it's
the ideal base to use for an exponential function .
• We derive the formula for compound interest, where the interest is compounded
n
times per year (the formula in the blue box at the top of page 342). We also
introduce
the formula for continuously compounded interest.
• When solving exponential equations and inequalities remember to take it slow
with
students. Remember to point out to them that our observation that ax > 0 for all
x is key to solving these equations and inequalities. Note that the book covers
only
exponential equations and does not cover inequalities.
Section 4.2: Section 4.2 introduces logarithmic functions. We'll do everything
in this
section.
Note: Students have more problems with logarithmic functions than with
exponential func-
tions. Many students have not seen logarithms in high school. This is their first
exposure
to the topic so please be mindful of that. Moreover, if they did see logarithms
before in
high school the experience usually leaves them scarred with mild to severe
logophobia and
recurring logarithmic nightmares. So don't be surprised if these students
approach the topic
with sheer terror or if they mumble the word \log" with a utter loathing and
disgust.
• Students don't have much trouble computing logs like log 216 or even
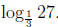But
they do have trouble computing things like ln e3 and ln
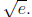Part of the problem is the
strangeness of the number e, but the main problem is the notation used for the
natural
logarithm. Many students just don't "see" ln x as
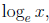even though they have
learned
that the two are the same. It might help some students to rewrite the ln
notation as
loge until they get used to it. Urge these students to use the
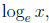notation
whenever
the ln x notation is confusing them. (Obviously, we will accept both notations
on a
quiz or an exam.)
• Students also have trouble graphing f (x) = ln x accurately. For reasons
unknown to
mankind, they have more trouble remembering the shape of ln x than the shape of
ex.
• Students often have trouble remembering/understanding these two identities:
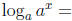
x and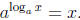 
Not surprisingly, they have even more trouble when the base
is e.
• The statement: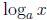
is the exponent to which a must be raised in order to
get x helps
students with computations.
• In practice, we won't ask students to graph any logarithmic functions where a ∈(0, 1).
• One thing to beware of here: the text writes that
this
notation was introduced in Section 3.5. Please don't use it. Just point out that
since
f(x) = ln x is increasing on (0,∞), the graph of f keeps rising as we move to
the right
and does not level off and approach a horizontal asymptote.
• You will see many students in this course (and even in math 10A and 10B) that
seem
to love to forget that ln 1 = 0
Section 4.3: This section is quite straightforward. We cover everything in this
section.
There is only one di±culty students have in this section, but it is a serious
one: they tend
to make up new \laws" of logarithms. They are actually more likely to do this in
Section
4.4, where they have to use these laws to solve equations, than they are in
Section 4.3,
where they are just doing exercises using the laws of logarithms. For example,
it is common
to see a student start solving an equation like ln(2x + 5) - ln(x - 2) = ln 6 by
writing
ln[(2x + 5) - (x - 2)] 
ln(x + 7) = ln 6. In this case, of course, the student
has applied
the " property " lnA - lnB = ln(A - B). Other all-time favorites:
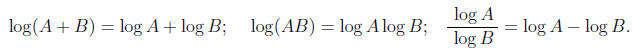
Be on the lookout for these in both Sections 4.3 and 4.4.
I also find it helpful repeating the rules of logs over and over and using the
following mantra:
"A product inside the log becomes a plus outside the logs" and so on for the
other rules.
• Despite what the text does in Example 2c on page 360 and elsewhere, we will
generally
not use a calculator to approximate the value of logarithms in answers to
problems.
Make sure that students know that if they get a final answer like ln 3 or log 25,
they
should just leave it in that form, unless we explicitly ask them to get a
decimal
approximation. Of course, they should simply things like ln 1 = 0
Section 4.4: We do everything in this section except solving equations
graphically (Solu-
tion 2 of Example 3, Solution 2 of Example 8, and Example 9). We also add some
logarithmic
equations and inequalities to the section.
Preliminary comments: This is actually the hardest section in the course for
students.
Students don't have much trouble with exponential equations, but they have a
whole lot of
trouble with logarithmic equations.
We'll concentrate mostly on equations involving ex and ln x, but we will also do
a few
equations with other bases.
Here's what we said to students in the reading notes about calculator use:
In this section, the text frequently uses a calculator to get a decimal
approxima-
tion of an answer. However, if you do a problem and your final answer contains
an exponential (like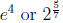 
) or a logarithm (like ln 6 or
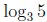), you should not
use a calculator to rewrite the answer as a decimal unless we explicitly ask you
to get a decimal approximation.
Here are some specific difficulties that I expect students to have have in this section:
• The mistake we see most frequently in this section is incorrect exponentiation
of both
sides of an equation. Here's a typical example:
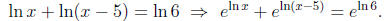
It's very hard to break some students of this habit (which, of course, reveals
that they
don't really understand how exponents behave).
• As I mentioned in Section 4.3, students also frequently make up new
"properties" of
logarithms. For example, it's common to see the following:
ln x + ln(x + 3) = ln 4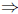 
ln (x + (x + 3)) = ln 4
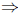ln(2x + 3) = ln 4.
• Students can also get confused when they have to use the two identities
ln ex = x and ln ex = x
in any but the simplest situations. A problem that's guaranteed to throw many
stu-
dents o® is the following: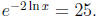 
Many students will simplify this as
-2x = 25.
Others will try to take the natural log of both sides (which is not wrong, but
which
usually leads to a mess.)
• Students also often forget to check that each solution of a logarithmic
equation is a
valid solution.
• Students get the idea that (in their words) "a logarithm can't be negative".
For
example, if you give them an equation like 3 ln x = - 6, some will say that there
are no
solutions. What they're doing, of course, is confusing input and output. It
might help
to say explicitly to them, whenever possible, that the input of a logarithmic
function
can't be negative but the output can.
• Logarithmic inequalities are not covered in the text. Students have a lot of
trouble with
these so take your time with them. The biggest problems for students: (1)
remembering
that their number line only consists of (0,+∞) and (2) finding good test points
to use.
The latter is the bigger problem. You'll need to emphasize that the most
effective test
points are powers of e.
| Prev | Next |