Matrix Notation
1 Matrix Basics
Recall that we can rewrite the system
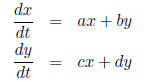
using matrix notation as
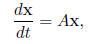
where
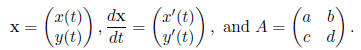
2 Matrix Operations
• Addition of matrices.
• Multiplying a matrix by a scalar.
• The product of a matrix and a column vector
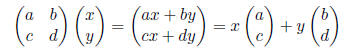
• The product of two matrices
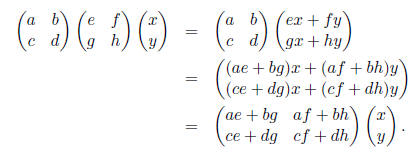
• AB = (Ab1,Ab2).
• In general, AB ≠ BA.
3 Solving a 2 × 2 Linear System
Consider the system
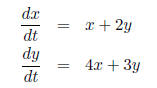
with initial conditions x(0) = 1 and y(0) = 1. For
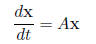
we can guess that the solution is of the form
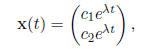
where λ, c1, c2 ∈ R.
4 Finding Eigenvalues and Eigenvectors
Let
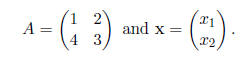
The system Ax =λx can be written as either
x1 + 2x2 = λx1
4x1 + 3x2 = λx2.
We can reduce this system to
(1 −λ)x1 + 2x2 = 0
(λ2 − 4λ − 5)x2 = 0.
Therefore, to obtain a nonzero solution either λ = 5 or λ = −1.
• If λ = 5, the first equation in the system becomes −2x1
+x2 = 0, and
we can let
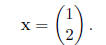
• If λ = −1, then
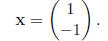
The number λ is called an eigenvalue of A, and x ≠ 0 is an eigenvector
corresponding to λ.
5 The Principle of Superposition
The Principle of Superposition tells us that any linear combination of
solutions
to a linear equation is also a solution. Therefore
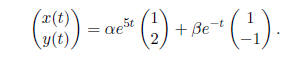
6 The Characteristic Equation
The key to solving the system
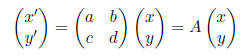
is determining the eigenvalues of A. To find this eigenvalues, we need to
derive the characteristic polynomial of A ,
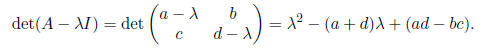
The quantity T = a + d is the sum of the diagonal elements of the matrix
A. We call this quantity the trace of A and write tr(A). Of course, D =
det(A) = ad−bc is the determinant of A. If a 2×2 matrix A has eigenvalues
λ1 and λ2, then the trace of A is λ1 + λ2 and det(A) = λ1 λ2. Indeed, we
can rewrite the characteristic polynomial as
det (A − λI) = λ2 − Tλ + D.
The eigenvalues of A are now given by
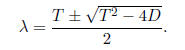
We can immediately see that the expression T 2 −4D
determines the nature
of the eigenvalues of A.
7 The Trace-Determinant Plane, D = T2/4
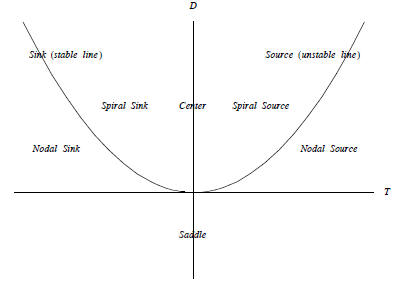
Figure 1: D = T2/4
| Prev | Next |