Vectors
Provides a vector orthogonal to two others
Magnitude provides sine of angle between u
and v
|sin(theta)|=|uxv|/|u||v|
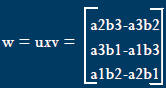
Applications to 3D Graphics
Vertex
Matrix
Identity
Rotation
Translation
Scale
Projection
Mathematics
Multiplication
Dot Product
Cross Product
Homogeneous Coordinates
In affine spaces points and vectors can be
confused
P=[x y z]T
V=[x y z]T
Instead use
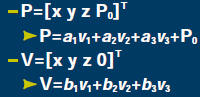
Affine transformations preserve lines
Points
 |
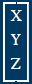Point, same notation as vector. Keep track of units |
 |
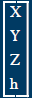Point |  |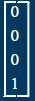
Origin |
 |
Specify Standard Space |
 |
Homogenized Point. Intersection with standard plane/space Fails when h=0 |
||
, three equations in 3D
Point- Slope Form
m=slope, (x,y)=point 0, 
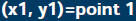
L=Q+tw
Point-Normal Form
L is the line
Q is a point on the line
t is the unknown
w is a directional vector for the line
w must be from one point to another
where 
is
the second point
Plane Equations
p=ax+by+cz+d
Three point form
p is the plane
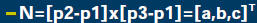(cross
product)
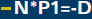(dot product)
p=(X-P)·v=0
Point-Normal form
X is unknown
P is point on plane
v is normal to plane
Line-Plane Intersections
Substitute for x , y, or z in 3 point form
Works well for slope intercept form
Substitute line for X in point normal form
Works well when line in point normal form
Carried out: t=(((P-Q)·v)/(w·v))w
Intersection point at: Q+(((P-Q)·v)/(w·v))w
t is time (unknown)
v, w are vectors
Q ,P,X are points
Translation Matrix
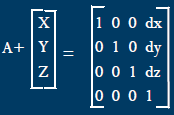
Rotation Matrix
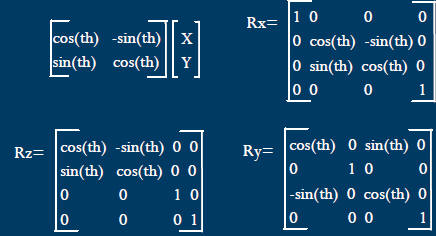
Scaling Matrix
Simple Perspective
Projection Matrix
Mutiple Transformations
Rotate about fixed point
S=(T)R(-T)p
Instance Transformation
Multiple uses of Same object
M=TRS
Order of operations
Right to left - fewer component operations
Precalculate matrix ops
Not unique effect but resulting matrix is
Rotations relative to
another angle
Translate to origin
Rotate to align with current orientation
Rotate by specified amount
Rotate to unalign with orientation
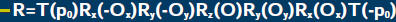
Rotation about an
arbitrary axis
Rotate to the axis first
Apply a rotation to the rotation
Brings it into the correct frame of reference or
orientation first
OpenGL
Provides 2 Frames
Camera frame, fixed
World frame
Current Transformation Matrix
Applied to everything
Changing CTM changes state of environment
4x4 Matrix
OpenGL Matrix Operations
Replacement Matrices
glLoadIdentity()
glLoadMatrixf(pointer to matrix);
Matrix Transformations
glRotatef(angle, vx, vy, vz);
glTranslatef(dx, dy, dz);
glScalef(sx, sy, sz);
glMultMatrixf(myarray);
Rotation about a
fixed point
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTanslatef(4.0, 5.0, 6.0);
glRotatef(45.0, 1.0, 2.0, 3.0);
glTranslatef(-4.0, -5.0, -6.0);
Matrices are generated left to right
Matrix farthest to the right is applied first
Matrix Stacks
Saving of states
Transform only part of a scene
Scale a single object
Rotate a heirarchical object
Apply transformation then restore original
state
glPushMatrix();
glScalef(3.0, 4.0, 5.0);
/* Draw Scaled Object */
glPopMatrix();
| Prev | Next |