12 Sets of Rules, Techniques, & Strategies Needed for Success in Elementary Algebra
1) Order of operations
1) parentheses (innermost 1st; & including absolute value)
2) exponents (including square roots )
3) multiplication or division (left to right)
4) addition or subtraction (left to right)
Tutorial example:
1) 5[8 – 2(4 – 1)] =
solution: 5[8 – 2(3)] = 5[8 – 6] = 5[2] = 10
2) Simplifying expressions
1) addition
a) when – only w/ like terms (same variables, same exponents)
b) how – add coefficients (missing coefficient is assumed to = 1), keep
exponents same
i) 3x2 + 5x2 = 8x2
2) multiplication
a) when – w/ like or unlike terms
b) how – multiply coefficients, add exponents of like bases (missing exponent is
assumed to = 1)
i) (4x2)(5x3) = 20x5
3) distributive property
a) when –
i) multiplying parentheses
ii) inside of which is addition or subtraction
b) how – distribute multiplication to each term inside
parentheses (terms are separated by + or – signs)
i) 2x3y(3x2 + 7xy3) = 2x3y(3x2) + 2x3y(7xy3) = 6x5y + 14x4y4
Tutorial examples:
1) 2x2 + 3x + 3 + y2 + 4x2 + x + y2 + 5 =
solution: 6x2 + 4x + 2y2 + 8
2) 3(y + 2) + 4y(2y + 1) =
solution: 3y + 6 + 8y2 + 4y = 8y2 + 7y + 6
3) Negative numbers
A) computation rules:
1) addition (same signs) – add, give same sign [ –2 + –7 = –9 ]
2) addition (different signs) – subtract, give sign of larger number [ –3 + +8 =
+5 ]
3) subtraction – change to addition of opposite, then follow addition rules [ –4
– –6 = –4 + +6 = +2 ]
4) multiplication & division (same signs) – answer is positive ( + + or – – = +)
[ (–2)(–7) = +14 ]
5) multiplication & division (different signs) – answer is negative ( + – or – +
= – ) [ (–3)(+8) = –24 ]
B) attach single sign to the term to the right (as positive or negative), and
treat as addition [ –3 –8 = –11 ]
C) absolute value:
1) geometrically – distance of number away from 0 (without regard to direction)
2) mechanically – strips sign away from number (number without sign is assumed
to be positive) [ | –4 | = 4 ]
Tutorial examples:
1) – | –6 + 8 | =
solution: – | + 2 | = –2
2) a2 + 3a – b2 – 4a2 + a – b2 + 9 =
solution: – 3a2 + 4a – 2b2 + 9
3) 3x[7 – 5(x – 2)] =
solution: 3x[7 – 5x + 10] = 3x[17 – 5x] = 51x – 15x2
4) Solving linear equations
1) simplify both sides
2) move variables & constants to opposite sides (by adding, to both sides, the
opposite of what you want to move)
a) if variables disappear
i) if what remains is identical, “all numbers”
ii) if what remains is not identical, “no solution”
b) if variables don’t disappear, then proceed
3) divide both sides by coefficient
Tutorial examples:
1) solve 5x – 3 = 8x + 3
solution:
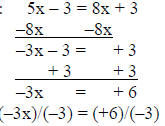
answer: x = –2
2) solve 2y + 4(y – 1) = 4(y + 1)
solution:
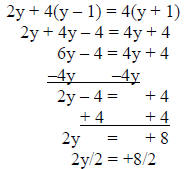
answer: y = 4
3) solve a + 3 = 2a – (a – 3)
solution:
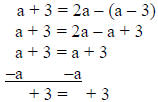
answer: all numbers
5) Algebraic fractions
1) reducing to lowest terms
a) can only cancel factors (things being mult), not terms (things being add or
subt)
2) equivalent fractions
a) determine what factors are missing in original denominator that exist in new
denominator
b) multiply numerator by same factors to achieve new numerator
3) multiplication
a) do not need LCD (Lowest Common Denominator)
b) cancel factors (if possible) – factor in numerator w/ factor in denominator
(cross-wise or straight up & down) c) multiply straight across
4) division
a) do not need LCD
b) change to multiplication by reciprocal (inverse) of 2nd fraction
c) follow multiplication rules above
5) addition/subtraction
a) need LCD (LCD is LCM of denominators – take most of each factor present in
any 1 denominator)
b) construct equivalent fractions w/ LCD (following above “equivalent fractions”
technique)
c) combine numerators over LCD
d) reduce to lowest terms (following above “reducing to lowest terms” technique)
6) equations (have right-hand side to =, as opposed to expressions which have no
right-hand side)
a) mult both sides of equation by LCD (distribute to each term)
b) cancel factors (in LCD w/ denominators) – should now have equation w/ no
fractions
c) solve linear equation (ck to make sure answer doesn’t make any denom = 0; if
so, throw out solution)
Tutorial examples:
1) [x3/(3y2)] ÷ [(x + y)/(12y3)] =
solution:
[x3/(3y2)] · [(12y3)/(x + y)] =
[x3(4y)]/(x + y) =
answer: (4x3y)/(x + y)
2) [3/(4ab)] + [(5a)/(6b2)] =
solution:
LCD = 12ab2
[3·(3b)/(4ab)·(3b)] + [(5a)·(2a)/(6b2)·(2a)] =
[9b/(12ab2)] + [(10a2)/(12ab2)] =
answer: (9b + 10a2)/(12ab2)
3) solve
[(2y)/3] – 5 = (5y)/6
solution:
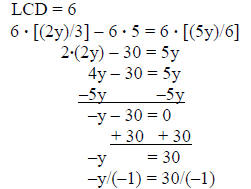
answer: y = –30
6) Solving & graphing linear inequalities
A) single inequalities (answer must have variable on left side)
1) move variable to left, constant to right (by adding the opposite of what you
want to move)
2) divide by coefficient (dividing by negative reverses direction of inequality
symbol)
3) graph will have shaded arrow going in same direction as inequality symbol
B) double inequalities (answer must have variable in middle, and both inequality
symbols pointing left)
1) isolate variable in middle by adding opposite of constants to all 3 parts
2) divide by coefficient in all 3 parts (dividing by negative reverses direction
of both inequality symbols)
3) graph will be shaded between 2 endpoints (w/ no shaded arrow)
C) endpoint(s)
1) strict inequality (< or >)
a) open circle
2) “or equal to” inequality (≤ or ≥)
a) closed (shaded) circle
Tutorial examples:
1) solve & graph 2x + 2 ≤ 3x
solution:
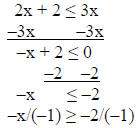
answer:
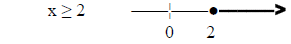
2) solve & graph –7 < 4x – 3 < 9
solution:
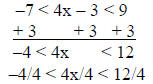
answer:
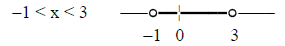
7) Graphing linear functions (using table of values)
1) 2 basic set-ups:
a) y is isolated on 1 side
i) choose x = 0 for 1st “easy” choice (substitute back into equation & solve
for y)
ii) choose x = 2 for 2nd “easy” choice (substitute back into equation & solve
for y)
b) x & y are on same side
i) choose x = 0 for 1st “easy” choice (substitute back into equation & solve
for y)
ii) choose y = 0 for 2nd “easy” choice (substitute back into equation & solve
for x)
2) plot 2 points [ordered pairs (x,y)] on Rectangular Coordinate System (x –
horizontal axis, y – vertical axis)
3) draw line thru 2 points
Tutorial examples:
1) graph y = 2x + 1
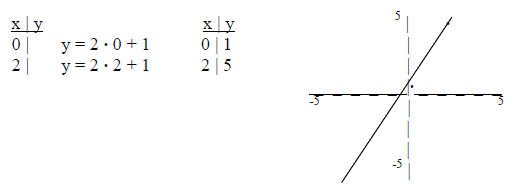
2) graph x + 2y = 4
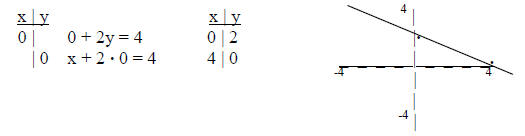
| Prev | Next |