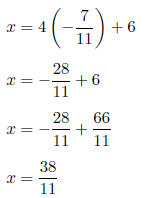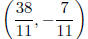SOLVING SYSTEMS OF LINEAR EQUATIONS BY THE SUBSTITUTION METHOD
SOLVING SYSTEMS OF LINEAR EQUATIONS BY THE SUBSTITUTION METHOD
Definitions:
• System of linear equations : consists of two or more linear equations
with the same variables.
• Consistent: The system is consistent if there is exactly one solution.
• Inconsistent: The system is inconsistent if there is no solution. This
happens when the two equa-
tions represent parallel lines .
• Dependent: The system is dependent if there is an infinite number of
ordered pairs as solutions.
This occurs when the two equations represent the same line.
Steps for the Substitution Method:
1. Choose one of the equations and solve for one variable in terms of the other
variable.
2. Substitute the expression from Step 1 into the other equation.
3. Solve the equation from Step 2. (There will be one equation with one
variable).
4. Substitute the solution from Step 3 into either of the original equations.
This will give the value of
the other variable.
Important Properties :
• The Substitution Method is useful when one equation can be solved very quickly
for one of the
variables.
• If the equation in Step 3 above is a false statement (such as 7 = 2), then the
system is inconsistent.
• If the equation in Step 3 above is a true statement (such as 0 = 0), then the
system is dependent.
Common Mistakes to Avoid:
• Remember that a system of linear equations is not completely solved until
values for both x and y
are found. To avoid this mistake, write all answers as an ordered pair .
• Remember that all ordered pairs are stated with the x- variable first and the
y-variable second,
namely, (x, y).
• If the first equation is used to solve for the variable, substitute it into
the second equation. Otherwise,
this will incorrectly lead to the statement 0 = 0.
PROBLEMS
|
1. Solve 2x + y = 5 3x + 2y = -8 Notice that the first equation can be solved easily for y, giving us 2x + y = 5 y = -2x + 5 This is what we will now substitute into the y variable in our second equation. This gives us: 3x + 2(-2x + 5) = -8 3x - 4x + 10 = -8 -x + 10 = -8 -x = -18 x = 18 Next, we need to find the value of our y variable by substituting x = 18 into one of the equations. Since we already know that y = -2x + 5, substituting in this equation gives us: y = -2(18) + 5 y = -36 + 5 y = -31
3. Solve
5. Solve
|
2. Solve 4x + 3y = 10 2x + y = 4 Notice that we can quickly solve for y using the second equation. 2x + y = 4 y = -2x + 4 We will now substitute this into the y vari- able in our first equation. 4x + 3(-2x + 4) = 10 4x - 6x + 12 = 10 -2x + 12 = 10 -2x = -2 x = 1 We now need to find the value of y by sub- stituting x = 1 into one of our equations. Since we already have that y = -2x + 4, substituting into this equation gives y = -2(1) + 4 y = -2 + 4 y = 2
|
||||
|
4. Solve
|
|||||
|
6. Solve
|
| Prev | Next |
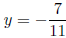
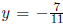 into one of our equa-
into one of our equa-