Adding and Subtracting Radical Expressions

Introduction
To add or subtract radical expressions , first simplify and then combine like terms .

Although it’s true that 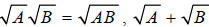is not equal to 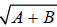. Students often miss
problems by applying this false “ rule .”

You can only add radicals if they are exactly the same. For example:

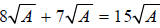
This is actually the distributive property at work. There’s a 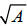factor in each term, so you can factor it
out:



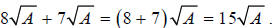
In fact, anytime you combine like terms the distributive property is involved.

Contrast the above with this expression: 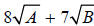. Here nothing can be factored out, and the two
terms cannot be combined. Leave them as is!

The comments above apply to all radicals - not just square roots .

Example A

Simplify: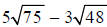

As always, factor the radicands

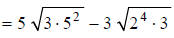
Divide the exponents in each of the radicals by the index, 2 , simplify, and combine like terms:

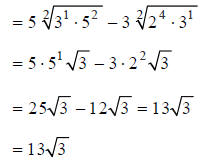
Example B
Simplify: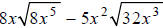

Factoring the radicands, we obtain:

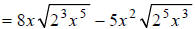
Dividing the exponents in the radicands by the index, 2 , we get:

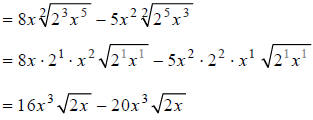
Combining like terms, we obtain:

Note that to be considered like terms, the variables outside the radical and their exponents also
have to be identical.

Example C

Simplify:

Factoring the radicands, we obtain:

Dividing the exponents in the radicands by 2 , we get:

Combining like terms:

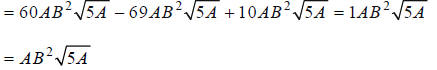
Extended Example 1a

Simplify: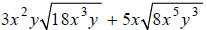

Hint: Factor the coefficients of the radicands .
Step 1:

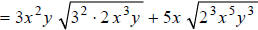
Hint: Divide the radicands' exponents by 2 . How many times does 2 go into each exponent, and
what is the remainder?
Step 2:

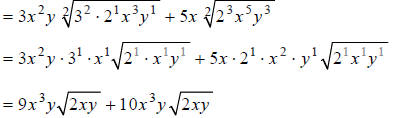
Hint: Combine like terms.
Answer:

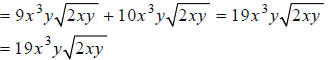
Extended Example 1b

Simplify: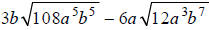

Hint: Factor the coefficients of the radicands.
Step 1:

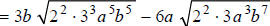
Hint: Divide the radicands' exponents by 2 . How many times does 2 go into each exponent, and
what is the remainder?
Step 2:

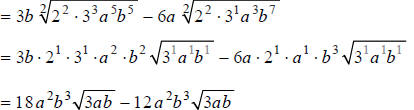
Hint: Combine like terms.
Answer:

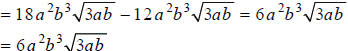
Extended Example 1c

Simplify: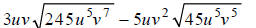

Hint: Factor the coefficients of the radicands.
Step 1:

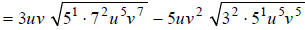
Hint: Divide the radicands' exponents by 2 . How many times does 2 go into each exponent, and
what is the remainder?
Step 2:

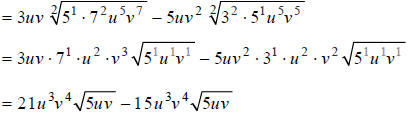
Hint: Combine like terms.
Answer:

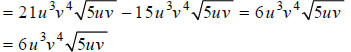
Example D
Simplify: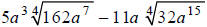

Factoring the coefficients of the radicands, we get:



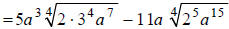
Next, we must divide the exponents in each of the radicands by the index, 4 . For each exponent,
you must decide how many times 4 goes into it, and determine the remainder:

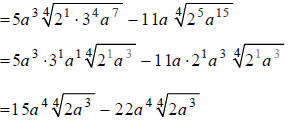
Combining like terms, we obtain:

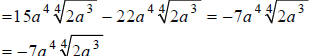
Example E
Simplify: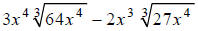

Factoring the coefficients of the radicands, we get:

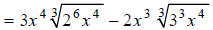
Next, we must divide the exponents in each of the radicands by the index, 3. For each exponent,
you must decide how many times 3 goes into it, and determine the remainder:

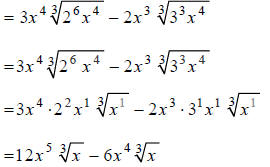
This time, the terms can’t be combined because they are not like terms. The x ’s outside the
radicals don’t have the same exponents.

Example F
Simplify: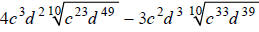

We must divide the exponents in each of the radicands by the index, 10 . For each exponent, you
must decide how many times 10 goes into it, and determine the remainder:

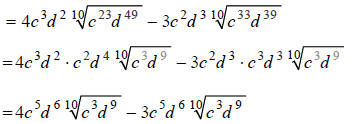
Combining like terms, we obtain:

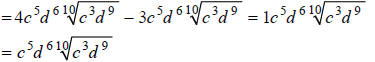
Extended Example 2a

Simplify: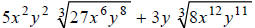

Hint: Factor the coefficients of the radicands.
Step 1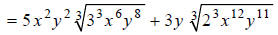

Hint: Divide the exponents in the radicands by 3. For each exponent, decide how many times 3
goes into it, and with what remainder.
Step 2:

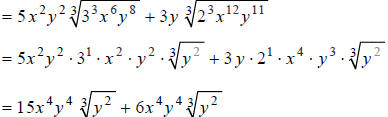
Hint: Combine like terms.
Answer:

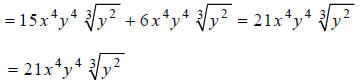
Extended Example 2b

Simplify: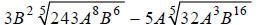
Hint: Factor the coefficients of the radicands.
Step 1:

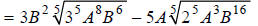
Hint: Divide the exponents in the radicands by5 . For each exponent, decide how many times 5
goes into it, and with what remainder.
Step 2:

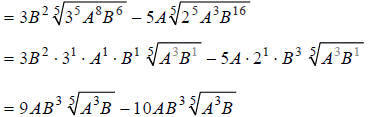
Hint: Combine like terms.
Answer:

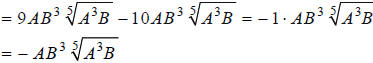
Extended Example 2c

Simplify: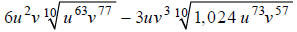

Hint: Factor the coefficients of the radicands.
Step 1:

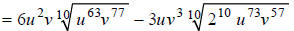
Hint: Divide the exponents in the radicands by10 . For each exponent, decide how many times
10 goes into it, and with what remainder.
Step 2:

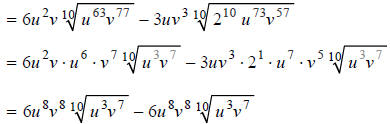
Hint: Combine like terms.
Answer:

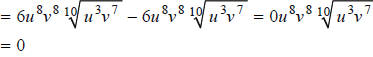
Our next example isn’t as scary as it looks. Just take it one step at a time…but first, take a deep breath!

Example G
Simplify: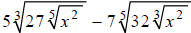

As usual, for our first step we factor all the coefficients under the radicals:

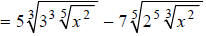
convert everything to fractional exponent notation:

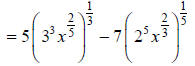
Distribute the fractional exponents, and simplify:

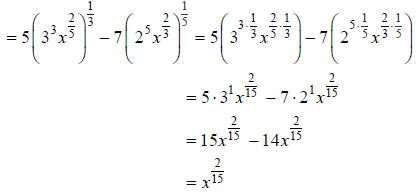
Example G, continued…

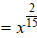
Finally, translate this back into radical form:

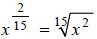
Notice what we accomplished in our last example. Each step was relatively simple, yet
we were able to simplify a cumbersome radical expression, revealing that

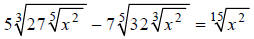
Rationalizing Denominators : Part 3

Consider the problem of rationalizing the denominator (which means eliminating radicals from the
denominator) of an expression such as

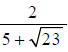
The techniques we studied earlier for rationalizing denominators don ’t work here. Whenever you have
two terms in the denominator, one or both of which is a square root , there’s a handy way to eliminate the
radical(s) by using the factoring formula a ² − b² = (a + b)(a − b) . On the left side of that equation,
each term is squared… and squaring gets rid of square roots!

The key is to multiply the numerator and denominator by the conjugate of the denominator. The
conjugate of a + b is a − b , and the conjugate of a − b is a + b .

Example H
Rationalize the denominator: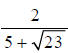

Multiplying the numerator and denominator by the conjugate of the denominator, we get:

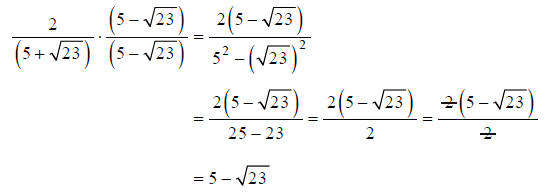
Though we set out only to eliminate radicals from the denominator, we ended up eliminating the
entire denominator! As Example H illustrates, rationalizing a denominator often results in a much
simpler expression.

Question: Rationalize the denominator: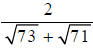

Answer: Multiply the numerator and denominator by the conjugate of the denominator, and
simplify.

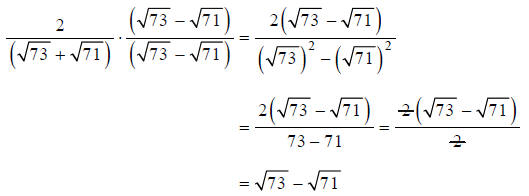
Question: Rationalize the denominator: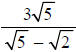

Answer: Multiply the numerator and denominator by the conjugate of the denominator, and
simplify.

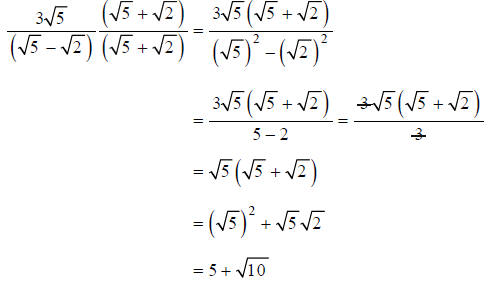
Question: Rationalize the denominator: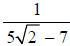

Answer: Multiply the numerator and denominator by the conjugate of the denominator, and
simplify.

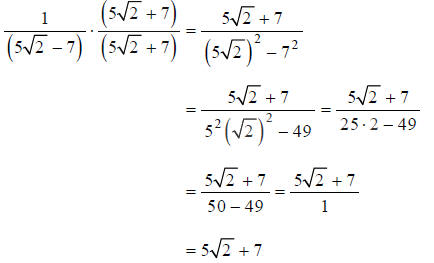
Example I
Rationalize the denominator: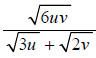

Multiplying the numerator and denominator by the conjugate of the denominator, and
simplifying, we get:

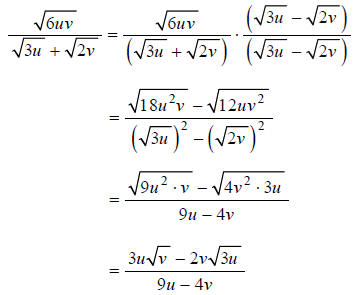
Don’t be tempted to cancel out anything in that last expression! Factors to be cancelled must be
factors of both the entire numerator and the entire denominator.

Question: Rationalize the denominator: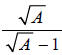

Answer: Multiply the numerator and denominator by the conjugate of the denominator, and simplify.

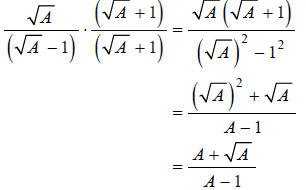
Question: Rationalize the denominator: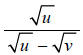

Answer: Multiply the numerator and denominator by the conjugate of the denominator, and simplify.

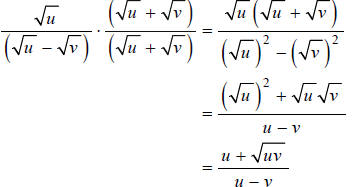
Question: Rationalize the denominator: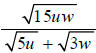

Answer: Multiply the numerator and denominator by the conjugate of the denominator, and simplify.

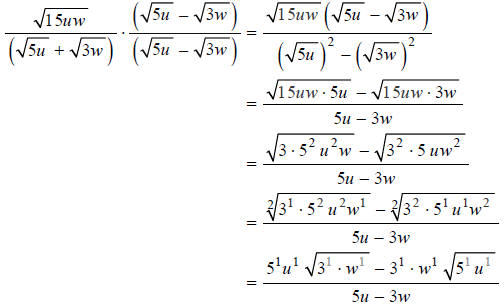
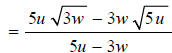
Don’t even think about cancelling
anything—there are no common factors to
cancel here!

Example J
Rationalize the denominator: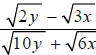

Multiplying the numerator and denominator by the conjugate of the denominator, and
simplifying, we get:

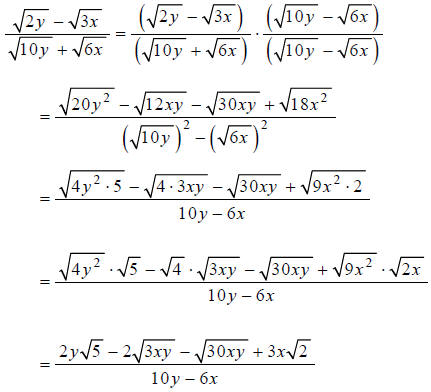
This can’t be simplified further.