Advanced Lecture Polynomials
Most algebra problems become straightforward to one armed with the following toolkit:
1 Vieta’s Formulas
If you think you haven’t seen Vieta(aka Viete)’s formulas in action , think
again. These
formulas are trivial to derive but are among the most useful tools for tackling
standard
polynomial problems. To understand Vieta, simply equate a polynomial to the
product of
its linear factors and a constant . To start, let’s consider the tame quadratic
with roots r1
and r2:
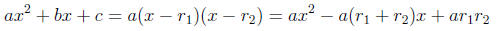
Equating coefficients, we see that:
a = a
b = −a(r1 + r2)
c = ar1r2
These are Vieta’s formulas, unsimplified. That’s all there is to it.
Similarly, for the cubic with roots r1, r2, r3, we get the following equality:
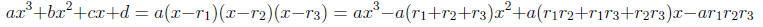
And similarly for the general polynomial with roots r 1, . . . , rn, we get that
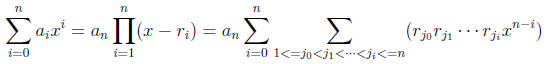
Specifically, the product of the roots is the coefficient of the constant
term divided by the
coefficient of the leading term times −1 if the polynomial has odd degree. The
sum of the
roots is minus the coefficient of the second term from the left divided by the
coefficient of
the leading term.
2 Finding Roots
A stereotypical algebra problem asks you to solve an equation . Luckily, for
polynomials this
is relatively easy. For quadratics and cubics there is a straightforward method.
For quartics
and above, you will usually have to employ a trick such as a substitution or a
geometric
interpretation.
2.1 Quadratic and Depressed Cubic Formulae
You should know that:
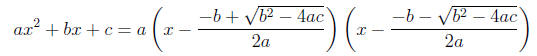
To depress the cubic equation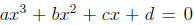
substitute
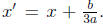This
will
eliminate the x ^2 term. Now divide by a and we get a cubic of the form x^3 + bx
+ c = 0. One
of the roots of this cubic is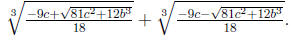
2.2 Rational Root Theorem
Let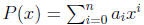
be
a polynomial and let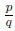
be
a reduced rational root of P. Then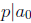
and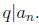
To prove this, consider the factorization of P(x).
3 Factoring Polynomials
In this section, completely factoring a polynomial will be defined as
expressing it as a product
of polynomials with integral coefficients that are all irreducible across the
integers by hand.
(No TI-89 factoring) Sometimes solving a problem comes down to your ability to
factor a
polynomial. True, factoring often comes down to guesswork, but then again, so do
differential
equations, and that’s a whole field in itself. You should view a factoring
exercise as a puzzle:
each term you factor out brings you closer towards the answer. Usually, there
will be a key
step of this puzzle , which is represented by a big factor. Sometimes you may
even have to
factor functions other than polynomials, but polynomials are typically the
hardest functions
to factor.
3.1 Tips and Trix
1. Always start by trying to factor out small things and make the resulting
polynomial
easier to work with. There’s almost always a linear factor . Difference of
squares is very
common.
2. Remember that (ax − b) is a factor of P(x) iff P( b/a ) = 0.
3. Roots of unity / cyclotomic polynomials are irreducible (if you don’t know
about this,
you should learn it, but it won’t be covered today)
4. Based on the problem’s context, is there something that should be a factor?
5. If your intuition says that the polynomial irreducible, then it probably is,
but don’t
forget about USAMO 2007/5(a one step factoring problem which nobody solved)!
3.2 Some polynomials to factor
Some of these might be irreducible. Hopefully these exercises will help
develop your factoring
intuition. Factor each of the following polynomials completely.
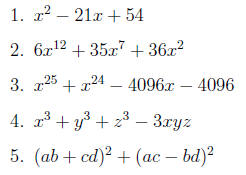
4 Problems
1. How many quintics are there whose roots are all 0 or 1?
2. Find all the real roots of x^3 + x + 2 = 0.
3. Let x, y, z be real numbers which add up to 0. Find all possible values of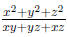
4. Find the sum of the squares of the roots of x^4 + 2x^3 − 3x^2 + 4x − 5 = 0.
5. Find all the real roots of x^4 + (2 − x)^4 = 34.
6. If x is real and x^3 + 4x − 8 = 0, find all possible values of x^7 + 64x^2.
7. Find the sum of the absolute values of the roots of x^4 − 4x^3 − 4x^2 + 16x − 8 = 0.
8. Suppose P(x) is a polynomial such that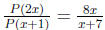
for
all x that keep both sides of
the equality defined. If P(1) = 1, find P(−1).
| Prev | Next |