Algebra 2 Unit Descriptions
The main theme in Algebra II is expanding the notion of a
function through the study of a variety of function types. Logic and
reasoning skills learned in Geometry continue to be applied in proving logical
statements about the various functions studied. The
function concept is thoroughly explored at the beginning of the course, and
properties of functions are highlighted. Knowledge of
quadratic equations and transformations is linked as quadratic functions are
graphed in the plane. The complex number system is
introduced as a way of describing certain solutions obtained from the quadratic
formula. The concept of the root or zero of a quadratic
function is connected to x- intercepts and expanded to polynomial functions and
the factor theorem. The difference between the
expansion (including the Binomial theorem) and factorization is highlighted. The
roots and graphs of polynomial functions are
thoroughly analyzed. Previous knowledge of circles and the graphs of quadratic
functions, provide the foundation for the study of
conic sections. The concepts of the rational numbers and rational expressions
are expanded to the analysis of rational functions. The
poles and asymptotes of a rational function are thoroughly explored, as well as
operations on these functions, and finding intersections
of these functions. The connections between inverses and compositions are made,
with a clear illustration of the relationship of the
domain and range of a function and its inverse. The concept of inverses is then
discussed in the context of radical functions. Rational
exponents are used to rewrite radical expressions. Inverses are also used to
establish the connection between exponential and
logarithmic functions. These functions are analyzed, and exponential and
logarithmic equations are solved in a real world context,
with a focus on exponential growth and decay and compound interest . Knowledge of
linear equations is needed for the study of linear
systems. Basic notions of counting and probability are then discussed.
Arithmetic and geometric series are discussed, as well as
methods of finding partial sums.
Unit Organization:
Unit 1: Functions and Equations in Two Variables
Unit 2: Analyzing Quadratic Functions
Unit 3: The Complex Plane
Unit 4: Analyzing Conic Sections
Unit 5: Analyzing Polynomial Functions
Unit 6: Analyzing Rational Functions and Equations
Unit 7: Compositions and Inverses
Unit 8: Inverses and Radical Functions
Unit 9: Analyzing Exponential & Logarithmic Functions
Unit 10: Modeling Linear Systems
Unit 11: Counting & Probability
Unit 12: Arithmetic & Geometric Sequences and Series
Unit 13: CST Review
Textbook: Larson, R., Bowell, L., Kanold, T.D., & Stiff, L. (2003). Algebra 2. Boston: Houghton Mifflin Company.
Unit 1: Functions and Equations in Two Variables
Algebra II begins with a discussion of the distinct, but closely related,
ideas of functions and equations. These concepts are analyzed
in a wide variety of examples throughout this course. A function is then defined
as a process that takes an input and produces an output,
such that for each allowable input, there is one and only one output. The domain
is defined the set of allowable inputs, and the range is
the set of outputs. These inputs and outputs may be numbers, people, or anything
else – examples of non-numerical functions are
explored (e.g. the function whose input is a person, and whose output is their
eye color). Function notation is introduced to represent
functions. The main focus of this course is the study of functions where the
inputs and outputs are real numbers. Examples of such
functions in the real world are given (e.g. population of the city as a function
of time). These functions can be represented numerically by
tables, and visually by graphs in the coordinate plane , where the process of the
function becomes to look up the input along the horizontal
axis, draw a vertical line up to the graph, and then draw a horizontal line to
the vertical axis to read off the output. These graphs may also
be represented by an equation in two variables, which is a mathematical
statement involving two variables (typically x and y) of the form
expression1 = expression2, which is true exactly when the point (x, y) is a
point on the graph. Linear functions and their graphs are
explored as examples of functions whose domain and range are the real numbers. A
root of a function is defined as a value that makes the
function zero. Roots of linear functions are estimated from the graph.
Just as not all functions can be described by an equation (e.g. non-numerical
functions), not all equations represent a function. The
equation of the circle of radius r with center (h, k), (x − h)2 + (y
− k)2 = r2 , is derived from the geometric definition of a
circle and the
distance formula, and the reasons why this equation cannot represent a function
are explored. This leads to a discussion of how to quickly
determine whether a graph (of an equation, or given on its own) represents a
function, namely the vertical line test.
Functions, their graphs and equations (such as y = x2) continue to be
analyzed, and equations that do not represent y as a function of x
(such as x = y2) are also investigated. It is emphasized that an
equation is simply a true/false statement (i.e. a Boolean expression), while
a function is an operator that produces an output from a given input. The domain
and the range of a function are discussed both
graphically and algebraically. Many different examples of the domain and range
are discussed, including functions with both finite and
infinite domains.
Piecewise functions (two parts) are then introduced to show that a single
function need not be represented by one simple equation . In
particular, the absolute value function requires knowing what part of the domain
contains the input, in order to evaluate the function.
Finally, new functions are developed from previously known functions using
addition, subtraction , multiplication and division .
| # | Learning Targets | Standard | Textbook Section |
Book Practice |
Active Practice |
| 1A | Explain the definition of a
function, and the meaning of the domain and range of a function. |
24.0 | 2.1 | Pg. 71 – 72; #1-4, 17, 19- 33, 51-55, 57 |
Gallery Walk (2), Round Robin |
| 1B | Give an example of a non-numerical
function, and state the domain, the range, and the rule. |
24.0 | T/F Strips | ||
| 1C | Give an example of a function whose
domain and range are the real numbers, and represent this function using a table and a graph. |
24.0 | TPS | ||
| 1D | Evaluate functions for given values of x. | 24.0 | 2.1, 2.7 | Pg. 71 – 74; #11-16, 18, 43-52, 56, 58- 62. Pg. 117; #13- 20. |
Function Bingo |
| 1E | Explain the definition of an equation. | 24.0 | |||
| 1F | Compare and contrast the concepts of a function and equation. | 24.0 | |||
| 1G | Graph a linear function, and
estimate the roots of a function from the graph. |
24.0 | 2.1 | Pg. 71 – 74; #5-10, 34-42. |
Mini- Whiteboards |
| 1H | Explain the relationship between the
roots of a function and the graph of the function, and give examples. |
24.0 | 2.3, 2.4 | Pg. 86-87; #16-18, 37-39. |
Mini- Whiteboards |
| 1I | Give two examples of equations that
do not represent functions, and graph each equation. |
17.0 | |||
| 1J | Determine if a graph represents a function using the vertical line test. | 24.0 | 2.1 | Pg. 72; #30-32. |
Gallery Walk |
| 1K | Graph and write a piecewise (two part) defined function. | 24.0 | 2.7 | Pg. 117-118; #21-26, 35, 37-38. |
Mini- Whiteboards |
| 1L | Explain the role of the domain in writing and evaluating a piecewise function. | 24.0 | 2.7 | Pg. 117-118; #21-26, 35, 37-38. |
Mini- Whiteboards |
| 1M | Graph the absolute value function,
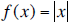 |
1.0 | 1.7, 2.8 | Pg. 54; #47-58. Pg. 125; #4-10, 12-17 |
|
| 1N | Add, subtract, multiply, and find the composition of functions. | 24.0 | 6.3 | Pg. 341-343; #2-71 |
Matrix, Gallery |
| 1O | Judge the validity of a logical
argument made about functions and their properties. |
25.0 | Embedded |
Essential Standards (CA):
Algebra 2:
24.0 Students solve problems involving functional concepts, such as
composition, defining the inverse function and performing arithmetic operations
on functions.
Supporting Standards (CA):
Algebra 2:
1.0 Students solve equations and inequalities involving absolute value.
17.0 Given a quadratic equation of the form ax2+ by2+
cx + dy + e = 0, students can use the method for completing the square to put
the equation into standard form
and can recognize whether the graph of the equation is a circle, ellipse,
parabola , or hyperbola. Students can then graph the equation.
25.0 Students use properties from number systems to justify steps in
combining and simplifying functions.
| Prev | Next |