Algebra Practice Test with Solutions
1. Rationalize the denominator:
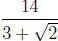 .
.
Solution:
Multiply the numerator and denominator by the conjugate of
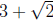 .
.
After simplifying, this gives 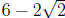 .
.
2. Given g(x) = 5x2 - 2x + 3 and 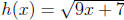 ,
find the value of (g o h)(2).
,
find the value of (g o h)(2).
Solution:
h(2) = 5 => g(h(2)) = g(5) = 118.
3. Find the sum or difference as indicated , and write your answer in simplified
form.
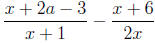
Solution:
Get a common denominator: (x + a)(2x).
After simplifying, this gives 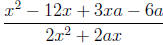
4. Factor and reduce to simplest form : 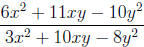 .
.
Solution:
Factoring the numerator and denominator gives 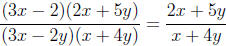 .
.
5. Simplify the following completely: 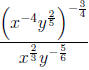 .
.
Solution:
Using properties of exponents, we get 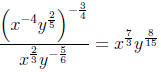
6. Perform the indicated operation and simplify your
answer:
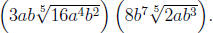
.
Solution:
Simplifying the radicals gives 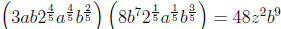 .
.
7. Solve the following equation: 5(x-7)2 -13(x-7)-6 = 0, then find the sum
of the roots.
Solution:
Let y = x-7. Solving the resulting quadratic equation and substituting back,
we get the sum of the roots is 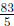 .
.
8. Solve for a: 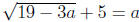 . and find the sum of all solutions.
. and find the sum of all solutions.
Solution:
Isolate the radical, square both sides, and solve the resulting quadratic equa-
tion. After checking each solution, we get the sum of the solutions is 6.
9. A radioactive element decays according to the model
y = 80e-0.21t, where t is in hours.
Use natural logarithms to find the half -life of the element.
Solution:
Half-life is the time when half of the original amount remains.
Solve the equation 80e-0.21t = 40 for t: e-0.21t= 0.5.
Take the natural logarithm of both sides: -0.21t = ln(0.5).
Divide by 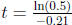 . The half-life is l
. The half-life is l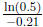 hours.
hours.
10. Fin d the point (x, y) that satisfies both equations.
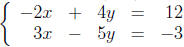
What is the value of x + y?
Solution:
Solving the first equation for y gives 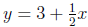 .
.
Substituting into the second equation and solving for x gives x = 24.
Thus, x + y = 39.
11. Two investments are made totaling $10,000. In one year
these investments
yield $650 in simple interest. Part of the $10,000 is invested at
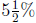 , and the
, and the
rest at 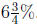 . How much more money is invested at
. How much more money is invested at
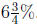 ?
?
Solution:
Let x be the amount invested at 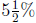 and y
be the amount invested at
and y
be the amount invested at 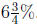 .
.
T he resulting system of equations is
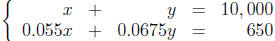 . Solve this system and find the difference
. Solve this system and find the difference
in the amounts invested: $6,000.
12. y = f(x) is a linear equation .
If f(3) = 5 and f(6) = 9, find the slope of the line.
Solution:
f(3) = 5 and f(6) = 9 means that the points (3, 5) and (6, 9) are on the line.
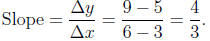
13. Write the equation (in slope- intercept form ) of the line with slope 5 which
passes through the point (-2, 3).
Solution:
The slope-intercept form of the line is y = mx + b. The slope is m = 5.
Substitute x = -2 and y = 3, then solve for b.
3 = 5(-2) + b
3 = -10 + b
13 = b
so y = 5x + 13.
14. Find the vertex of the function f(x) = (7p)x2 + (28p)x + (11p).
Solution:
Using the formula for the vertex of a parabola, we get x = -2.
Then f(-2) = -17p and the vertex us (-2,-17p).
15. Beginning with 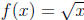 , nd the function g(x) that shows f(x) shifted to
, nd the function g(x) that shows f(x) shifted to
the left 2 units, reflected about the x axis, and then shifted up 7 units.
Solution:
The function f(x) shifted to the left by 2 units is
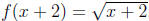 .
.
Reflecting about the x-axis is
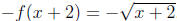 .
.
Then, shifting this up by 7 units gives g(x) = -f(x+2)+7 =
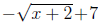 .
.
16. Given these three equations, select the true statement below.
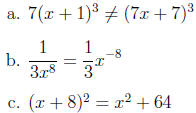
Solution:
a. is true: 7(x+1)3 = 7(x+1)(x+1)(x+1) = (7x+7)(x+1)(x+1) but
(7x + 7)3 = (7x + 7)(7x + 7)(7x + 7)
b. is true: 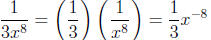
c. is false: (x + 8)2 = (x + 8)(x + 8) = x2 + 16x + 64
17. Find the domain of 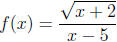 .
.
Solution:
The expression under the square root sign must not be negative.
The denominator may not be equal to 0.
This means both x + 2 ≥ 0 and x - 5 ≠ 0
so x ≥ -2 and x ≠ 5.
18. 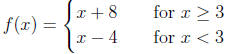
Find f(0).
Solution:
To evaluate the piecewise-defined function, we must decide which piece to use.
"Find f(0)" means to find the y-value when x = 0.
Since x = 0 and 0 < 3, we use the second piece.
Plug x = 0 into the second piece: f(0) = 0 - 4 = -4.
19. Find the x-intercept(s) of the function
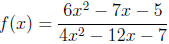 , if any exist.
, if any exist.
Solution:
Factoring and setting the numerator equal to zero gives
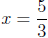 .
.
20. Solve for x using the quadratic formula: x2 - 6x + 2 = 0.
Simplify as much as possible.
Solution:
The quadratic formula is 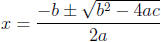 .
.
With a = 1, b = -6, and c = 2 this gives
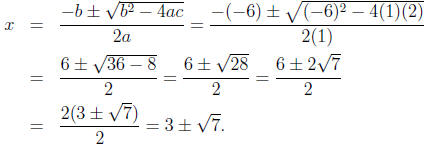
21. Solve for x: 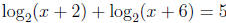 .
.
Solution:
Using the properties of logarithms, simplify, and then convert to exponential
form to get x2 + 8x = 12 = 32. Solving this quadratic equation and checking
the roots gives x = 2.
22. Simplify the following expression: 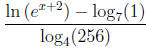
Solution:
Using properties of logarithms, we get 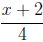 .
.
23. Given 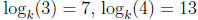 , and
, and
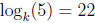 , find
, find
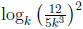 .
.
Solution:
Expanding according to the rules of logarithms , we get
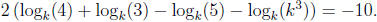
24. Solve for x: 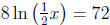 .
.
Solution:
Isolate the ln, convert to exponential form , and solve for x. Thus, x = 2e9.
25. A real estate developer opens a new subdivision with a certain number of
houses. Each year, 12 new houses are built in the subdivision. The number of
houses in the subdivision is a linear function of the years since the
subdivision
opened. Seven years after opening, there were 109 houses. Eleven years after
opening, there were 157 houses.
How many houses were there at the beginning? What are the units of the
slope of the line?
Solution:
Points are (t, y), where t is the number of years since the subdivision opened,
and y is the number of houses in the subdivision.
We have (7, 109) and (11, 157): The slope of the line through these points is
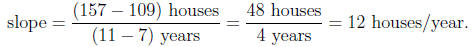
The equation of the line through (109, 7) with slope m = 12 is
y - 109 = 12(t - 7)
y - 109 = 12t - 84
y = 12t + 25
When t = 0, y = 25, so there were 25 houses initially.
The units of the slope of the line are houses per year.
26. Write the exponential function which represents the data in this table.

Solution:
The function is an exponential function because the ratio of the f(x)-values
is 4. Also, f(0) = 0.2.
The equation, then, is f(x) = 0.2(4)x.
| Prev | Next |