Algebra Review
3 Gaussian integers and quaternions; sums of two squares and
four squares
Definition 3.1 The Gaussian Integers are complex numbers of the form {a+bi : a,
b ∈ Z}
where
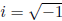 . They form the ring Z[i]. The norm of z ∈ Z[i] is
. They form the ring Z[i]. The norm of z ∈ Z[i] is
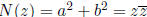 .
.
Exercise 3.2 Define divisibility among Gaussian integers. Observe that z
|w => N(z) |N(w).
Show that the units among the Gaussian integers are ±1,±i.
Exercise 3.3 Use Gaussian integers to show that
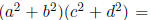 sum of two
squares .
sum of two
squares .
Hint. Observe that N(zw) = N(z)N(w).
Exercise![]() 3.4 Define division with remainder among
Gaussian integers. Show the existence
3.4 Define division with remainder among
Gaussian integers. Show the existence
of g.c.d. ’s. Use this to establish unique prime factorization in Z [i].
Exercise 3.5 Show: if z is a prime in Z[i] then N(z) is either p or p2 for some
prime p ∈ Z.
In the former case p = N(z) = a2 + b2; in the latter case, p = z.
Exercise![]() 3.6 Let p ∈ Z be a prime. Prove: p is a prime in Z[i] if and only if p
≡-1
3.6 Let p ∈ Z be a prime. Prove: p is a prime in Z[i] if and only if p
≡-1
(mod 4). Hint. “If:” if p ≡-1 (mod 4) then p ≠ a2 + b2. “Only if:” if p ≡1 (mod
4) then
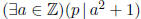 . Let w = a + bi ∈ Z[i]. Let z = g.c.d. (p,w).
. Let w = a + bi ∈ Z[i]. Let z = g.c.d. (p,w).
Exercise 3.7 Infer from the preceding exercise: if p is a prime (in Z) and p ≡1
(mod 4)
then p can be written as a2 + b2.
Exercise![]() 3.8 The positive integer
3.8 The positive integer 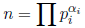 can be
written as a sum of two squares if and
can be
written as a sum of two squares if and
only if 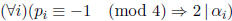 .
.
Exercise![]() 3.9 Show that the number of ways to write n as a2 + b2 in Z is
3.9 Show that the number of ways to write n as a2 + b2 in Z is
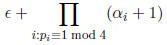
where ε = 1 if n is a square and 0 otherwise.
Exercise 3.10 Let n be a product of primes ≡ 1 (mod 4) and suppose n is not a
square.
Prove: the number of ways to write n as a2 +b2 is d(n) (the number of positive
divisors of n).
Definition 3.11 The quaternions form a 4-dimensional division algebra H over R,
i. e., a
division ring which is a 4-dimensional vector space over R. The standard basis
is denoted by
1, i, j, k, so a quaternion is a formal expression of the form z = a+bi+cj+dk.
Multiplication
is performed using distributivity and the following rules :
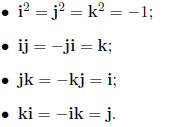
It is clear that H is a ring. We need to find inverses.
Exercise 3.12 For z = a+bi+cj+dk, we define the norm of z by N(z) = a2 +b2 +c2
+d2.
Prove: 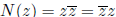 , where
, where
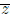 = a - bi - cj - dk is the conjugate quaternion.
= a - bi - cj - dk is the conjugate quaternion.
Exercise 3.13 Let z,w ∈ H. Prove: N(zw) = N(z)N(w).
Exercise 3.14
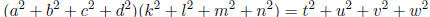
where t, u, v,w are bilinear forms of (a, b, c, d) and (k,
l, m, n) with integer coefficients . Calculate
the coefficients .
Exercise* 3.15 (Lagrange) Every integer is a sum of 4 squares. Hint. By
the preceding
exercise, it suffices to prove for primes. First prove that for every prime p
there exist
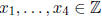 such that p
such that p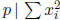 and g.c.d.
and g.c.d. 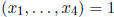 . Let now m > 0 be minimal such
. Let now m > 0 be minimal such
that 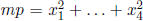 ; note that m < p. If m ≥ 2, we
shall reduce m and thereby obtain
; note that m < p. If m ≥ 2, we
shall reduce m and thereby obtain
a contradiction (Fermat’s method of infinite descent; Fermat used it to prove
that if p ≡ 1
(mod 4) then p is the sum of 2 squares). If m is even, halve m by using
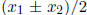 and
and
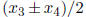 (after suitable renumbering). If m is odd,
take
(after suitable renumbering). If m is odd,
take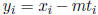 such that
such that
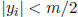 .
.
Observe that 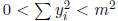 and
and
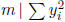 , so
, so 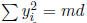 where 0 < d < m. Now represent
where 0 < d < m. Now represent
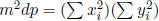 as a sum of four squares,
as a sum of four squares,
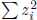 , using the preceding exercise . Analyzing
, using the preceding exercise . Analyzing
the coefficients, verify that 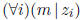 . Now
. Now
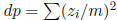 , the desired contradiction.
, the desired contradiction.
4 Fields
Definition 4.1 A field is a commutative division ring.
Example 4.2 Let F be a field.
• 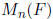 := set of n × n matrices over F is a ring
:= set of n × n matrices over F is a ring
• 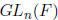 := group of units of
:= group of units of
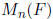 is called the “General Linear Group ”
is called the “General Linear Group ”
Exercise 4.3 A finite ring with no zero divisors is a division ring.
(Hint: use Exercise 2.13.)
Theorem 4.4 (Wedderburn) A finite division ring is a field.
Exercise 4.5 If F is a field and 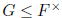 is a
finite multiplicative subgroup then G is cyclic.
is a
finite multiplicative subgroup then G is cyclic.
Definition 4.6 Let R be a ring and for x ∈ R let
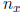 be the g.c.d. of all n such that nx = 0
be the g.c.d. of all n such that nx = 0
where
nx := x + . . . + x when n > 0
nx := −x − . . . − x ( n times ) when 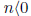
nx := 0 (n times) when n = 0.
Exercise 4.7 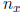 ·
x = 0
·
x = 0
Exercise 4.8 If R has no zero divisors then
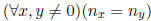 .
.
Definition 4.9 The common value 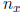 is
called the characteristic of R.
is
called the characteristic of R.
Exercise 4.10 If R has no zero divisors then char(R) = 0 or it is prime.
In particular, every
field has 0 or prime characteristic.
Exercise 4.11 If R is a ring without zero-divisors, of characteristic p,
then (a+b)p = ap+bp.
Exercise 4.12
1. If R has characteristic 0 then R 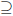 Z
Z
2. If R has characteristic p then R 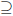 Z/pZ.
Z/pZ.
Exercise 4.13 If F is a field of characteristic 0 then F
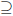 Q.
Q.
Definition 4.14 A subfield of a ring is a is a subset which is a
field under the same operations.
If K is a subfield of L then we say that L is an extension of K; the pair (K,L)
is referred to
as a field extension and for reasons of tradition is denoted L/K.
Definition 4.15 A prime field is a field without a proper
subfield.
Exercise 4.16 The prime fields are Q and Z/pZ (p prime).
Definition 4.17 Observe: if L/K is a field extension then L is a vector
space over K. The
degree of the extension is [L : M] := dimK L. A finite extension is an
extension of finite
degree.
Exercise 4.18 The order of a finite field is a prime power. Hint. Let L be a
finite field and
K its prime field, so |K| = p; let [L : M] = k. Prove: |L| = pk.
Exercise 4.19 The degree of the extension C/R is 2. The degree of the
extension R/Q is
uncountably infinite (continuum).
Exercise![]() 4.20
Prove that
4.20
Prove that 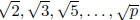 are linearly independent over Q.
are linearly independent over Q.
Exercise 4.21 If K
![]() L
L
![]() M are fields then [M :
L][L : K] = [M : K].
M are fields then [M :
L][L : K] = [M : K].
| Prev | Next |