ALGEBRAIC EQUATIONS
OVERVIEW:
The purpose of this project is to familiarize students with the idea of
“Algebraic
Equations” and their solutions. Algebraic Equations project is geared towards
grade level
9th – 12th.This project contains the definition of an equation and concept of
variables in
length. Classification of equations is done on different basis like degree of
equations,
number of variables and reducible equations . Solving of linear equations and
quadratic
equations is explained by different methods such as;
• Substitution Method
• Elimination Method
• Graphical Method
• Discriminant Method
RATIONALE:
Equations play a very dominant role in the study of any branch of science, arts,
environment, economy or educational puzzles. By the word equation, literally
speaking,
we mean the equality of two statements . For example, when a number is added to
the
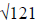 ; it becomes equal to 20.The unknown number is assigned a letter symbol “x”
and
; it becomes equal to 20.The unknown number is assigned a letter symbol “x”
and
problem is given a mathematical model and solved for the value of variable “x”.
Equations always involve variables. Equations involving only one variable are
called
equations in one variable, like wise in two variables x and y: three variables
x, y and z. In
solving simultaneous equations usually we need as many numbers of equations as
we
have the variables.
For Example,
• x + y = 5 will have many solutions but if the same equation is solved
simultaneously with x + 3y = 7, we need two equations and system can be solved.
x = 4 and y = 1 is the only unique solution.
Substitution Method: The substitution method is used to
eliminate one of the variables
by replacement when solving a system of equations. Think of it as "grabbing"
what one
variable equals from one equation and "plugging into the other equation.
For Example,
• x + y = 5 and x + 3y = 7
Using this method, one variable is expressed in terms of another:
y = (5 – x)
Plugging in the value of y in other equation
x + 3 (5 – x) = 7
Solving for x, we get x = 4
Plugging in the value of x in y = 5 – x gives y = 1.Therefore, (4, 1) is the
solution.
Elimination Method: In this method, coefficients of one of the variables are
made equal
by multiplying with suitable numbers to the two equations and by adding or
subtracting
one of the variables is eliminated.
For Example,
• 2x + 3y = 10
5x - 2y = 6
In the above system of equations, to make the coefficients of y equal, we
multiply the
top equation by 2 and bottom equation by 3 and add:
4x + 6y = 20
15x – 6y = 18
_____________________
19x = 38, x = 2
Again plugging in the value of x in top equation, we get, 4 + 3y = 10 , y =
2.Therfoere , (2,2) is the solution.
Another classification of equations is based on the degree
of polynomial involved in
the equation. We name different degree equations by different names such as;
• x + 2 = 7 ( Linear, because degree of polynomial involved is 1)
• x2 + x – 6 = 0 ( Quadratic, because degree of polynomial involved is 2)
• x3 +3x2 +3x + 1 = 0 ( Cubic, because the degree of polynomial involved is 3)
• x4 -1 = 0 (Biquadratic, because the degree of polynomial involved is 4)
As the degree of equation increases, the complexity in solving or finding the
different solutions ( or roots) also increases .The most simple type of
equations in
single variable is linear equation in one variable i.e. ax + b = 0 , where a is
not equal
to 0.This is the general equation in one variable.
The goal of writing about the linear equations and quadratic equations is to
make
our learners succeed in this challenging and changing world. To expand the
knowledge of the use of linear equations, and how the equations reflect the
different
ways people work and learn together, students will be prepared both for the real
world challenges and their studies in mathematics at college and higher level
studies.
The unit on Linear Equation is a part and parcel of “School District of
Philadelphia” curriculum for 9th – 12th graders. Unit on linear equations
involved in
two variables can be explained by different methods fitting into the curriculum
for 9th
and 10th graders. However, the quadratic equations are explained for higher
levels
because of the involvement of requisites like; real and imaginary solutions.
Less
emphasis is drawn upon complex roots of quadratic equations.
Linear equations can be used almost at all levels of studies, depending upon the
mathematical modeling of the problems .Linear equations are at the very heart of
Algebra. An equation is always treated like a balance with its two pans always
balanced about the pivot. One can make changes of any type on both the
sides of the sign of equality. Different types of manipulations can be performed
on
both the sides of an equation: such as,
1. Addition
2. Subtraction
3. Multiplication
4. Division, with the exception of dividing by zero
5. Taking the positive square root with the exception of square root of a
negative
number
6. Doing the inversion
Example:
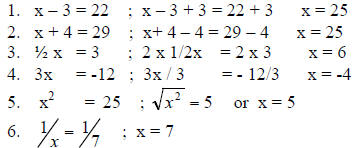
Examples (1) - (6) correspond to above mentioned
manipulations.
Another type of linear equation systems can be obtained by using two variables
or
three variables for which we need two simultaneous or three simultaneous
equations to
solve the systems .For Example: x + y = 13; x – y = 7 is a linear equation
system in two
variables x and y which can be solved together to give x = 10, y = 3 .However,
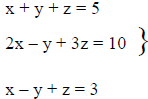 |
is a system of linear equations in three
variables x, y and z which can be solved together to give x = 1, y = 1 and z = 3. |
It is very important for the students to acknowledge that
some problems can be solved
without concentrating much on the linear equations. The students may need to
define
variables and write equations for the simplest of problems to feel comfortable
specially
when they encounter difficult equations .The following steps are encouraged when
one
encounters a difficult equation;
a) Choose the variable you are going to use in each problem and state what it
represents.
b) Write an equation, using your variable that represents the problem.
c) Solve the equation and the problem using any method you wish, including guess
and check ( also called trail and error method)
For Example:
1) A chef puts several batches of cubes into a cauldron. The first batch
contained 27
cubes and the last batch contained 56 cubes .A total of 108 cubes were put into
the
cauldron. How many cubes did the chef throw that were not part of first or last
batch?
Solution: Let us consider the number of cubes that chef
throws and were not the part of
first or last batch be “x” (a variable).
Therefore;
27 + x + 56 = 108 (writing an equation)
x + 83 = 108 ( combining the like terms )
x + 83 – 83 = 108 – 83 (solving for the variable)
x = 25 (solution)
Thus, the chef threw 25 cubes that were not the part of first or last batch.
Check 27 +25+56 = 108 (True)
Therefore, the solution is correct.
Example # 2:
Each adult needed 5 yards of shoelace for the trip to California and each child
needed 3
yards. A certain family with seven children needed 71 yards of shoelace. How
many
adults were in the family?
Solution: Let number of adults in the family be “x” (assigning a variable)
Therefore,5x + 3 x 7 = 71 (Writing an equation)
Or, 5x + 21= 71
Or, 5x + 21 – 21 = 71 – 21
Or, 5x = 50 (Solving the Equation)
x = 10
Thus, there were 10 adults in the family.
CHECK:
5 x 10 + 3 x 7 = 50 +21 = 71 (True)
Therefore, the solution is correct.
We have seen that a linear equation in one variable such as 3x + 4 = 2 (x – 1)
has
a unique solution i.e. x = -6.The equation x + 2y = 5 + 3x + y is also a linear
equation, but it includes two variables and has more that one solution. The
solutions of
such an equation can be found easily by assigning one variable in terms of
other. For
example, the above equation can be simplified to y = 2x + 5 and y has been
expressed in
terms of x. Assigning different values to variable “x” ,
we can determine different values
for variables “ y ”.

However, if these points or ordered pairs (0, 5), (1, 7),
(2, 9) …………are plotted
on a graph sheet and joined by a ruler, they make a straight line. A straight
line is made
up of an infinite number of points, so each point on the line corresponds to
solution of
this equation. So, we can conclude a linear equation in two variables has many
solutions.
Review that the term linear has both a “geometric” and an “algebraic” meaning.
Geometrically, linear means, a straight line and algebraically, linear means,
the degree of
variable used in the equation is one. For example x + 2y = 5 is linear but
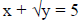 is
is
non – linear.
Exercise:
A. Classify the following as linear or non – linear equations
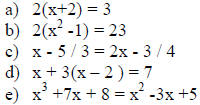
Answers:
a) Linear
b) Non Linear
c) Linear
d) Linear
e) Non linear
Exercise:
B: Solve the following linear equations in one variable
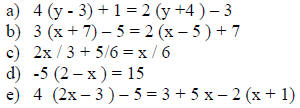
Answers:
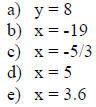
QUADRATIC EQUATION
Another class of equations is called “Quadratic equations in one variable” .The
most
general quadratic equation is ax² + bx + c = 0; where, a is not equal to 0 and
a, b, c are
real numbers and “x” is a variable. All the quadratic equations do not find
their solutions
in the real number system. It depends upon the value of “ b2-4ac” which is
called the
Discriminant of the quadratic equation. If b2- 4ac is negative, solution of
quadratic
equation is not present in real number system but is present in complex number
system
(beyond the scope of this project). However, the nature of solutions or nature of
the roots
of the quadratic equation can be discussed with the help of discriminant.
1. If discriminant is positive, the solutions or roots are real and unequal
2. If discriminant is negative, the solutions are non–real
3. If discriminant is zero, the solutions are equal
Examples:
1. 2x2 – x – 6 = 0; b2-4ac = 49 > 0, the roots are real and unequal and by
solving
we get x = 2 and -3/2.
2. x2 + x + 6 = 0 b2-4ac = -23 < 0, no real roots.
3. x2-6x +9 = 0 ; b2-4ac = 0 , the roots are equal i.e. x = 3 and 3.
Solution of a quadratic equation will be explained by different methods in the
chapter at a
later stage.
OBJECTIVES:
The main objective of this unit is to master the concept of linear equations and
quadratic
equations.
A. To explain and make students acquainted with the definition of linear and
quadratic equations.
B. To explain the meaning of solution of an equation
C. To explain with examples the different methods of solving linear equations
and
explaining the advantages of using one method over the other :
• Graphical method of solving two simultaneous linear equations
• The substitution method
• The elimination method
D. To explain the number of solutions of different systems of linear equations
• Consistent system – unique solution
• Inconsistent system - no solution
• Dependent system – many or infinite solutions
E. List of standards is given in the lesson plans
STRATEGIES:
The above mentioned objectives can be achieved by using different strategies
like,
a) Alternative teaching strategy
b) Interdisciplinary connection
c) Inclusion strategy
d) Enrichment
e) Co- operative learning
For example, using the “alternative teaching strategy” for graphical
method of solving a linear equation system, the teacher may display a set of co
– ordinate
axes on the over head. A point (1/2, 5/2) may be plotted on the graph. The
students are
asked to write the equations of two lines that pass through the point. The
students
participating in the discussion will come out with different equations of lines.
For Example,

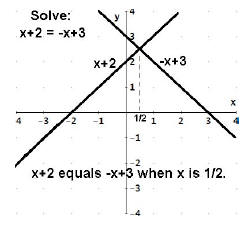
Example # 2:
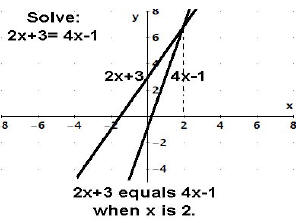
2x + 3 = 4x - 1
The two expressions "2x + 3" and "4x - 1" don't mean the same thing but there
may be a
time when they are equal. They are equal, the lines cross, when x is 2, and only
when x is
2.
The solution is 2.
An effective “Interdisciplinary general education program”
regularly reviews its goals, its curriculum, and the courses which it offers. In
addition, the
program has a process for regularly monitoring progress toward achieving
integrative
goals and outcomes, curriculum, and courses.
The students are asked to plot the graph of these equations and to their
surprise
both lines pass through the point (1/2, 5/2).Questions for students: Is there
any other point
where these two lines intersect or pass through? The prompt answer is: No. thus
the
response is elaborated to define the system of equations. The system of
equations with a
unique solution is called “Consistent system.”
Like wise for the “Inclusion strategies”, have students write each
equation in a system with a pencil of different colors. Then tell them to graph
each
equation in the corresponding color. Suggest that they use
a third color to draw the point
of intersection and to write the co – ordinates of that point.
“Enrichment” is the most effective strategy for students to research on a
problem. For Example, An increasing number of American households are choosing
to
obtain their television reception through a satellite dish rather than a cable.
A question
then arises, is it always beneficial for the household to get a satellite
connection over
cable? The answer to this depends on certain time factors . For instance, in a
locality one
company markets satellite service for an initial fee of $300; this included the
purchase of
dish and installation, and then charges $20 per month for programming. A cable
television company in the same area requires an initial fee of $14 for
installation and $31
per month thereafter. Ask students to solve system of equations
C = 300 + 20 t (For Dish Network company)
C = 14 + 31 t (For Cable - network company)
When the students solve the system, they get t = 26 and C= 820.it means the
cost of two networks for 26 months is the same i.e. $820.Now if a person wants
to reside
in that area for only 20 months ( less than 26 months) or forever, which type of
service is
better?
Research showed that cable company will charge the person $ (14 + 31 x 20) =
$634 while dish company will charge the person $ (300 + 20 x 20) = $700 for 20
months.
So the conclusion of research work is cable – network is better for the time
period of less
than 26 months while dish network is better for time period of more than 26
months.
CLASS ACTIVITIES
(LESSON PLANS)
OBJECTIVES
a) Solving equations by adding and subtracting
b) Solving equations by multiplying and dividing
c) Solving two-step equations
d) Solving multisteps equations
e) Using distributive property
f) Using formulas and literal equations
CONTENT /PERFORMANCE
a) Simplify multi-step problems involving positive exponents
b) Perform calculations requiring multiple procedures and operations involving
whole numbers, decimals, fractions and percents.
c) Represent given information as expressions, equations, inequalities, systems
of
equations, systems of inequalities, or matrices.
d) Determine the number of solutions that exist for a given system of equations.
e) Classify and describe system of equations.
f) Demonstrate recognition of the graphic representations of system of linear
equations and determine their solutions.
PA Standards (refer to standards alignment):
2.1 A Page 4; 2.2 A Page 6; 2.6 C Page 34; 2.8 D Page 36; 2.8 F, 2.8 G, 2.8 H
Page 38.
Textual References and Structural Lessons: Holt Algebra 1: Chapter1: Page 4 -49;
Chapter 2: Page 54- 108; Chapter 3: pp 135 – 153; Chapter 7; Pp 318-337
Technology: Page: 316-D.
Calculator keystroke guide, P – 789
Portfolio activities: pp – 325, 337
Curriculum Resources:
Chapter – pp 116-120
Other Instructional Resources/Technology:
Lesson Activities, pp 14-16
Cooperative – Learning Activities, pp.14-16
Student Technology Guide, pp. 14 – 16
Mathepedia CD- ROM
Writing Activities for your Portfolio, pp.7-9
Sample Assessment Item:
Simplify:
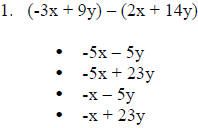
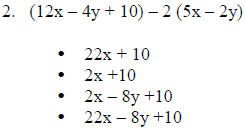
3. Solve for x: -6x + 7 = 5x + 62
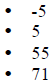
4. Romeo is constructing a border around his vegetable
patch. He wants the length to
be four times the width . He has only 100 feet of border material. Can he build a
border that is the length and the width he wants and that uses all of his border
material? Show your work and explain your solution.
Equations are the building blocks of algebra and help the
students in modeling
arithmetical problems to algebraic problems to algebraic problems by involving
equations.
For Example;
A boy has 28 coins in all, in dimes and nickels and when he counted the total
value of
coins, it came out to be $2.00.How many dimes and nickels the boy has?
If this problem is solved arithmetically using hit and trail method, it is time
consuming and boring because he will have to start at some dimes and nickel, say
5
dimes and 23 nickels and check the value, 6 dimes and 22 nickels and so on. Here
algebra
helps you. Let us assume that the boy has x number of dimes and y number of
nickels.
Then according to the data in question
x + y = 28 ……………………………(1)
And
10x + 5y = 200………………………. (2)
Equation (2) can be written as an equivalent equation by dividing throughout
by 5.So system of equations is reduced to:
x + y = 28 ……………………………. (1)
And
2x + y = 40 ………………………….. (2)
Solving the system by any convenient method: x = 12, y = 16 on check, we find
that the boy has 12 dimes and 16 nickels. So there are applications of equations
to
connect them to real world situations.
The same problem could have been solved by using one variable too. Let us
assume the number of dimes with the boy be X. So number of nickels will be (28 –
x) .For
the value equation 10x +5 (28 – x) = 200.Solving for X, we get the solution X =
12.Therfore, the number of dimes is equal to 12 and the number of nickels is (28
– 12)
i.e. 16.
| Prev | Next |