The Cubic Equation
[Pinter, Charles C. A Book of Abstract Algebra ,
McGraw-Hill, Inc. New
York, 1990.]
Recall the quadratic formula solved for the roots of a quadratic polynomials;
that is polynomials of the form
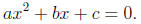
All the roots are given by the formula:
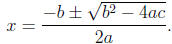
There is a general formula for cubic polynomials , those of the form
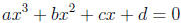
and the quartic
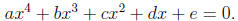
However there can be no other formulas – in part because
any number
greater than 4 determines certain things called groups with properties related
to polynomials that can never be fixed. Here we will explore the
cubic equation.
To begin with, any cubic polynomial can be written as
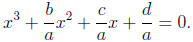
For convenience we will relabel our letters as
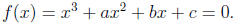
1. Begin by substituting
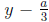 in for x. You may want to try this with
in for x. You may want to try this with
some actual numbers first . Once you have checked you will realize
that
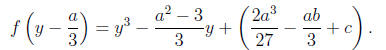
Notice the x2 term is gone ! This trick is incredibly
useful because
now instead of finding roots of f(x) we will only care about roots of
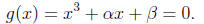
Keep in mind the roots of g will be different form those
of f, but we
know that
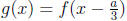 so we can go back at the end.
so we can go back at the end.
2. Finally g(x) is a nicer polynomial, nice enough to have
a cubic formula.
One of the roots will be given as
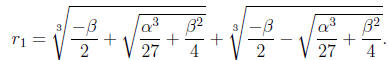
It is particularly more difficult to derive this formula
but you may check
with some polynomials to see that you agree.
3. You have one root 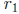 so you can divide you polynomial g(x) by
so you can divide you polynomial g(x) by
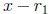
to get a quadratic polynomial . Here you simply use the quadratic
equation to solve for the remaining roots.
4. Now you have to translate all the roots into roots for f(x) by subtracting
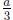 from each.
from each.
| Prev | Next |