Application of Matrix Operations
A graph consists of a set of vertices and a set of edges
that connect
(some of) the vertices. The arrows on the edges distinguish between
two -way connections and one-way connections. Such a graph can be
described by an n × n matrix called an adjacency matrix in which 1’s
and 0’s are used to describe connections. Specifically, if the vertices
are labeled from 1 to n, then the entry in row i and column j of the
adjacency matrix is a 1 if there is a connection from vertex i to vertex
j, and a 0 if there is not.
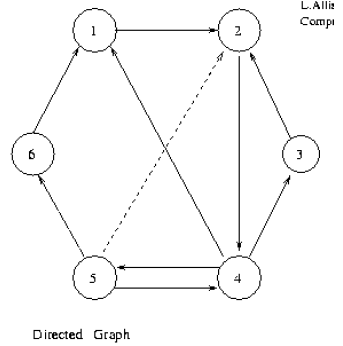
Construct the adjacency matrix for the graph in the following figure,
and let A denote the matrix. Compute A2, A3, and A4, and interpret
the results in terms of the graph . Try to generalize the meaning of An
for positive integers n.
Note: this problem is related to the Bridges of Konigsberg
problem,
posed to Leonhard Euler in the mid 1700s by the citizens of the Prus-
sian city of Konigsberg (now Kaliningrad in Russia). The
city is cut by
the Pregel River , which encloses and island, as shown in the following
figure:
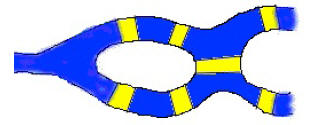
The problem was to determine whether it was possible to
start at
any point on the shore of the river, or on the island, and walk over
all of the bridges, once and only once, returning to the starting spot.
In 1736 Euler showed that the walk was impossible by analyzing the
graph .
| Prev | Next |