Beginning Algebra Chapter 6 Factoring Worksheet



Complete the factoring.

Factor.


Complete the factorization.

Factor.

Find all natural numbers that can replace b and make the expression factorable .


Factor.

Factor the sum of cubes .

Factor.

Factor completely.

Solve using the zero product property.

Solve.

Solve the problem .
51) Find three consecutive integers such that the square of the sum of the
smaller two is 45
more than the square of the largest.
52) The product of two consecutive integers is 71 more than their sum. Find the integers.
53) The length of a rectangle is 6 inches more than its width. If 3 inches
are taken from the
length and added to the width , the figure becomes a square with an area of 121
square
inches. What are the dimensions of the original figure?
54) A rectangular garden is three times as long as it is wide. If the area of
the garden is 2352
ft2, find the length and width of the garden.
Solve the problem . Round to the nearest tenth, if necessary.
55) If an object is thrown upward with an initial velocity
of 48 ft/sec, its height after t sec is
given by h = 48t - 16t2. Find the number of seconds before the object
hits the ground.
56) If an object is propelled upward from a height of 64
feet at an initial velocity of 96 feet per
second, then its height after t seconds is given by the equation h = -16t2
+ 96t + 64, where h
is in feet. After how many seconds will the object reach a height of 208 feet?
Answer Key
Testname: CARSON GILLESPIE JORDAN CHAPTER 6 PRACTICE PROBLEMS NOV 15 2006
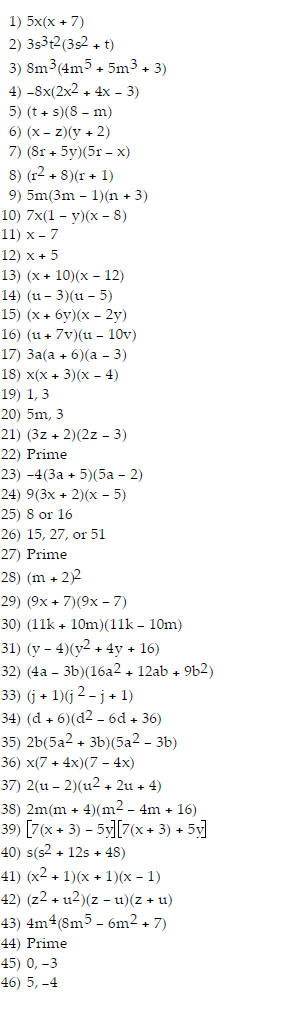
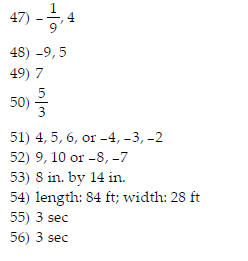
| Prev | Next |