Calculus II

Material to remember
There is a certain amount of mathematics that you have to remember, and have at you finger-
tips, in order to understand the lectures and be perform well on the exams. The are many
techniques for remembering information, for example using flash cards or association. Personally, I
think it is best to remember a few fundamental things, and be able to work out the less fundamental
things from these. Also, the more cross-links you have, the better you remember. If you forget
one bit of information but remember a cross-link, then you can generally recover the missing
information. Students who have a poor understanding of the subject matter, and have not sorted
the fundamental points from the less fundamental ones, attempt to remember everything. This
technique frequently fails in stressful situations (i.e. exams), especially when you have poorly
developed cross-links. Even if your short term memory is particularly good, and you can get
through the exam with a good grade, then you will have troubles in the next course that has the
previous course as a prerequisite (because then you need long term memory, and that does not
work with huge amounts of poorly sorted information). Much of the information below is from
precalculus. I encourage you to create your own summary (with cross-links) for all your courses
in mathematics.

Trigonometric Identities

(1) cos² θ + sin² θ = 1
(2) 1 + tan² θ = sec² θ
(3) cot² θ + 1 = csc² θ

I like to define cos θ and sin θ by the rule that (cos θ, sin θ) is the point on the circle x ²+ y²= 1
inclined at an angle of θ to the positive x-axis. Then (1) is merely Pythagoras’ Theorem. Equations
(2) and (3) follow from (1). Dividing both sides of (1) by cos²θ gives (2), and dividing both sides
of (1) by sin²θ gives (3).

Euler’s Formula 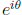= cos θ + i sin θ where i²= −1.

Addition Formulas Expanding 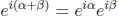and equating real and imaginary parts gives

(4) cos(α + β) = cos α cos β − sin α sin β,
(5) sin(α + β) = sin α cos β + cos α sin β.

The formula for tan (α + β) is obtained by dividing (5) by (4) and then dividing the numerator
and denominator by cos α cos β to get

(6)

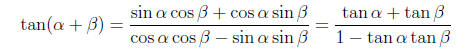
I do not remember the formulas for cos(α−β), sin(α−β) and tan(α−β). These can be deduced
from (4)–(6) by replacing β by −β and recalling that cos(−β) = cos β, sin(−β) = −sin β and
tan(−β) = −tan β (this last equation follows, of course, from the other two ). We tend not to use
addition formulas for sec, csc and cot.

Double-Angle Formulas Expanding 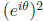and equating real and imaginary parts of
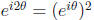
gives

(7) cos(2θ) = cos²θ − sin²θ = 2 cos²θ − 1 = 1 − 2 sin²θ,
(8) sin(2θ) = 2 sin θ cos θ.

The second and third expressions for cos(2θ) were obtained from the first by using sin² θ = 1−cos² θ
and cos² θ = 1 − sin² θ. Alternatively, put α = β = θ into (4) and (5). Dividing (8) by (7) and
then dividing numerator and denominator by cos² θ gives

(9)

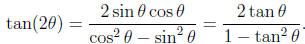
In Math 172.2 we shall use the half-angle formulas to convert a trigonometric integral to one
involving a rational function of t:

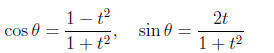where t = tan(θ/2).

Properties of a ^x and log_a x Let a be a positive base, a ≠ 1. Remember that log_a y = x means
a^x = y. Remember the graphs of y = a^x, and the inverse function y = log_a x, and how to change
base from a to e using the formulas 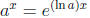and log_a x = ln x/ ln a. Also, (ab)^x = a^xb^x.

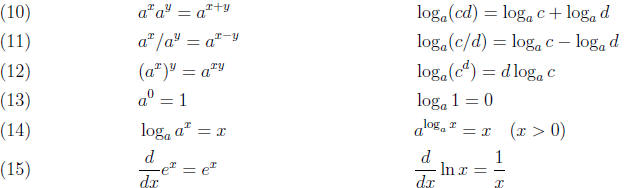
You need not remember (2) as it follows from (1) by replacing y by −y, and d by d^-1.

Derivatives You must remember the product, quotient and chain rules. You should be able to
deduce the quotient rule from the product and chain (or composite) rules. A common mistake is
to use the wrong numerator: uv′ − u′v instead of vu′ − uv′.

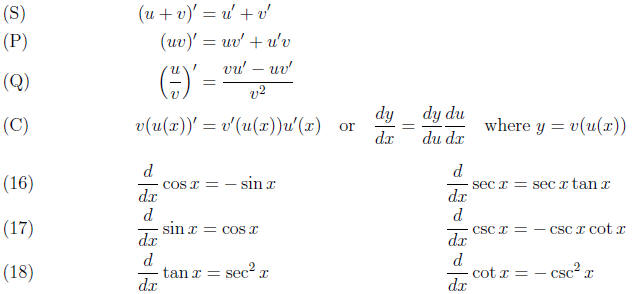
You have to remember the derivatives of cos x and sin x. You should be able to work out the
derivative of tan x using the quotient (or product) rule, and the derivatives of sec x, csc x, cot x
by differentiating (cos x)^-1, (sin x)^-1, (tan x)^-1 using the chain rule.

Completing the square This technique is used to writing a quadratic ax² + bx + c in the
form a(x − h)² + k. It is used in this course to evaluate integrals, and is used in precalculus to
find the vertex of a parabola , or the center and radius of a circle which is not in standard form
(x − h)² + (y − k)² = r². Completing the square is done as follows:

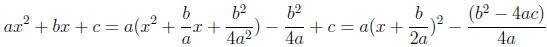
For example, 2x² − 12x + 17 = 2(x² − 6x + 9) − 2 × 9 + 17 = 2(x − 3)² − 1.

Polynomial division You should be able to divide one polynomial into another and find the
quotient and remainder. For example, dividing 2x² + 1 into 2x³ − 6x² + 5x − 4 gives a quotient
of x − 3 and a remainder of 4x − 1. These four polynomials are connected via the equation
2x³ − 6x² + 5x − 4 = (x − 3)(2x² + 1) + (4x − 1).

Definitions/Theorems You should remember every definition. The derivative is defined to be:

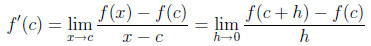
Note that f′(c) is the slope of the tangent line to y = f(x) at x = c.

DMVT If f(x) is continuous on the closed interval [a, b] and differentiable on the open interval
(a, b), then there exists a c in (a, b) such that

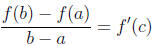
Arithmetic sums An arithmetic progression has first term a, and subsequent terms are obtained
by adding a fixed term d. Thus a, a + d, a + 2d, a + 3d, . . . , a + (n − 1)d is a typical arithmetic
progression. An arithmetic sum can always be computed by adding the sum forwards and
backwards. For example, to evaluate 1 + 3 + 5 + · · · + 101:

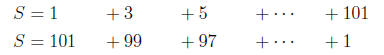(sum is independent of order of addition)

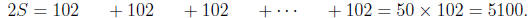
Therefore, S = 2550. In general, an arithmetic sum is the half the number of terms times the sum
of the first and last terms, e.g.

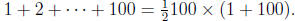
Formulas/Theorems You should remember the formulas for: the volume of a solid of revolution
(using the disc and shell methods ), the length of a curve, the surface area of a surface of revolution,
and the centre of mass of a rod with density ρ(x):

(disc method; about x-axis)
(shell method; about y-axis)
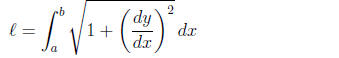(length)
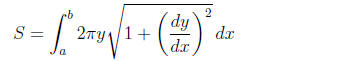(surface area)
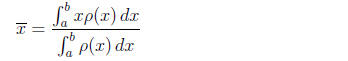(center of mass = moment/mass)

You should be able to state the major theorems of the course. Stating a theorem is more than
writing down a formula, you must specify the hypotheses and the conclusion clearly using words.
For example,

FTC1 Let y = f(t) be continuous on the interval [a, b] and let x be an element of [a, b]. The
derivative of the area function 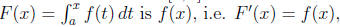or equivalently

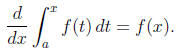
FTC2 If f(x) is continuous on [a, b] and F′(x) = f(x), then
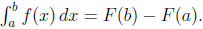
IMVT If f(x) is continuous on [a, b], then there exists a c in [a, b] such that

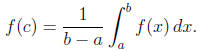
Integrals Of course, equations (15)–(18) can be written backwards as integral formulas, so you
need not remember these. You should remember

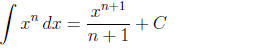(n ≠ −1),
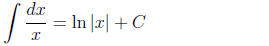(compare Eqn (15)),
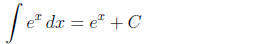(compare Eqn (15)),

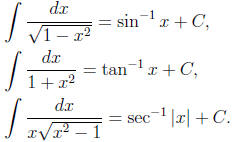
Techniques Four important techniques for antidifferentiation are (1) the substitution method (the
chain rule backwards), (2) integration by parts (the product rule backwards), (3) partial fractions
(adding fractions backwards), and (4) trigonometric substitution. Know how to compute improper
integrals (integrals with infinities in limits or integrand). In some years you may also be expected
to know how to integrate in polar co-ordinates. (I do not expect you to remember the formulas
for computing areas and arc lengths using polar coordinates .) It is good to try the above methods
in order, i.e. (1) first and (4) last. The following expressions 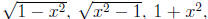suggest
the trigonometric substitutions x = sin θ, x = sec θ and x = tan θ respectively. The motivation
behind these substitutions is Eqns (1) and (2).