Combinations of Functions
Objective: In this lesson you learned how to find
arithmetic
combinations and compositions of functions.
I. Arithmetic Combinations of Functions (Pages 229-230)
| What you should learn How to add , subtract , multiply , and divide functions |
Just as two real numbers can be combined with arithmetic
operations , two functions can be combined by the operations of

to create new functions. A combined function like this is called
an arithmetic combination of functions.
The domain of an arithmetic combination of functions f and
g
consists of . . .
Let f and g be two functions with overlapping domains.
Complete the following arithmetic combinations of f and g for all
x common to both domains:
1) Sum : ( f + g)(x) =

2) Difference : ( f - g)(x) =

3) Product : ( fg)(x) =

4) Quotient: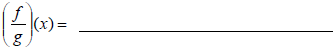
Example 1:
Let f (x) = 7x - 5 and g(x) = 3 - 2x .
Find
( f - g)(4) .
II. Composition of Functions (Pages 231-232)
| What you should learn How to find the composition of one function with another function |
The composition of the function f with the function g is
defined
as ( f o g)(x) =

For the composition of the function f with g, the domain
of
( f o g) is . . .
For two functions f and g, to find ( f o g)(x) , . . .
Example 2:
Let f (x) = 3x + 4 and let g(x) = 2x2 -1. Find
(a) ( f o g)(x) and (b) (g o f )(x) .
III. Applications of Combinations of Functions (Page 233)
| What you should learn How to use combinations of functions to model and solve real -life problems |
The function f (x) = 0.06x represents the sales tax owed
on a
purchase with a price tag of x dollars and the function
g(x) = 0.75x represents the sale price of an item with a price tag
of x dollars during a 25% off sale. Using one of the combinations
of functions discussed in this section, write the function that
represents the sales tax owed on an item with a price tag of x
dollars during a 25% off sale.
| Homework Assignment Page(s) Exercises |
| Prev | Next |