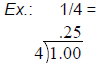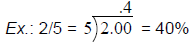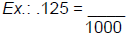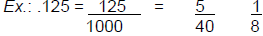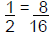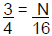Compass Math Sample

Converting Fractions , Decimals, and Percents

Changing Decimals to Percents (%):
• Move the decimal two places to the right and add the percent sign
Ex.: .25 = 25%

Changing a Percent to a Decimal:
• Move the decimal two places to the left and remove the percent sign (%)
Ex.: 25% = .25

Change a Fraction to a Decimal :
• Divide the numerator (top number) by the denominator (bottom number)

Change a Fraction to a Percent:
• Convert fraction to a decimal (see above Ex.)
• Move the decimal point two places to the right and add a percent sign (%)

Change a Decimal to a Fraction:
• Determine the place value of the last number in the decimal
Ex.:
.0 = tenths
.00 = hundredths
.000 = thousandths
.0000 = ten thousandths

• Write the place as the denominator (bottom number).

• Write your decimal without the decimal point as your numerator (top number).

Change a Percent to a Fraction:
• Change your percent to a decimal (see above).
• Change decimal to a fraction (see above).
Ex.: 40% = .4 = 4/10 = 2/5

1. Fill in the empty boxes.

Decimal	Fraction	Percent (%)
.25
	5/8
		50%
	2/3
.45
		30%
	1/5
.75

PERCENTS

Percent problems are made up of four elements:
1. The WHOLE is the number value after the word Of
2. The PART is listed before or just after the word IS
3. The PERCENT always has a percent sign (%)
4. All percents are based on 100
5. The PERCENT of the WHOLE is the PART

Solving for PART :
1. Identify the parts
2. Place the known information on a grid
3. Multiply the diagonals
4. Divide the answer by the number that is left
Ex.: What is 30% of 770?

Part ?	Percent 30
Whole 770	100 100

770 x 30 = 23100
23100 ÷ 100 = 231
Answer: 30% of 770 is 231

1. What is .5% of 300?

2. 65% of 240 is what?

3. 32% of the vote has been counted. If 775 people voted, how many votes have been
counted so far?

4. Kim bought a desk for $55.00. After she refinished it, she sold it at 250% of its
original price. What did she sell it for?

5. 38% of the families in the neighborhood are against having a gas station nearby. If
200 families are in the area, how many are against having a gas station?

Solving for PERCENT:
1. Identify the parts
2. Place the known information on a grid
3. Multiply the diagonals
4. Divide the answer by the number that is left
5. Add the percent sign
Ex.: 13 is what % of 25

Part 13	Percent ?
Whole 25	100 100

13 x 100 = 1300
1300 ÷ 25 = 52
Answer: 13 is 52% of 25

1. 62 is what percent of 124?

2. 83 is what % of 332?

3. Out of the 51 questions on the test, Tom answered 34 correctly. What percent of the total is
that?

4. Sue pays $14.40 a month in union dues. She earns $1800 a month. What percent of this
monthly pay goes to union dues?

5. The Johnson's paid $2320 in property tax on their $160,000 home. What % is their tax rate?

Solving for the Whole:
1. Identify the parts
2. Place the known information on a grid
3. Multiply the diagonals
4. Divide the answer by the number that is left
Ex.: 50% of what is 290.

Part 290	Percent 50
Whole ?	100 100

290 x 100 = 29000
29000 ÷ 50 = 580
Answer: 50% of 580 is 290

1. 175% of what is 770?

2. 844 is 80% of what?

3. Max paid $42 tax on the furniture he bought. If the sales tax was 7%, what was the
cost of the furniture?

4. To buy a house, the Smiths need a down payment of 20%. They have saved
$25,000. What is the most the Smiths can pay for a house?

5. Joyce received a $6.75 tip. It was 15% of the cost of the meal. What was the cost of
the meal?

Ratios

• Relating part of an amount to the whole or another part
Ex.:
You have a basket of 20 balls: 9 white and 11 red
What is the ratio of white balls to the red balls? 9 (white balls) 11 (red balls)?

Proportion

• A statement comparing two ratios
Ex.: 1 is to 2 as 8 is to 16

Solving for the Unknown in Proportions :

• N is the missing number
• Find the cross product of the numbers you know (multiply diagonally)
Ex.:
3 x 16 = 48
4 x N = 4N
48 = 4N
• Divide each side by the number that is with the unknown (N)
48 ÷ 4 = 12
4N ÷ 4 = N
Answer: N = 12