Fibonacci and Square Numbers

Introduction

Fibonacci is one of the best-known names in mathematics, and yet Leonardo of Pisa (the name by
which he actually referred to himself) is in a way underappreciated as a mathematician. When
hearing the name we are most likely to think of the Fibonacci sequence, and perhaps Leonardo's
problem about rabbits that began the sequence's rich history. Leonardo's role in bringing the ten-digit
Hindu-Arabic number system to the Christian nations of Europe might also come to mind. While these
two contributions are undoubtedly enough to guarantee him a lasting place in the story of
mathematics, they do not show the extent of Leonardo's enthusiasm and genius for solving the
challenging problems of his time, and his impressive ability to work with patterns of numbers without
modern algebraic notation . In this article, we will try to shed light on this side of Leonardo's work by
discussing some problems from Liber quadratorum, written in 1225, using the English translation The
Book of Squares made by L. E. Sigler in 1987. All page references in what follows are to that book

Questions for student investigation are at the end of this article

The Court of Frederick II

The Book of Squares is addressed to Frederick II , the Holy Roman Emperor, ruler of Germany and
southern Italy. The outline of Leonardo's life is given elsewhere on this web site, but it is worthwhile
to consider the context of this particular work in more detail. Frederick II had a tremendous hunger
for knowledge. In spite of his German roots, he was most at home in Sicily, an intersection point for
Latin, Greek, and Arabic culture. Scholars from all three were brought to his court. Frederick was
called stupor mundi, " the wonder of the world," because his behavior was so astonishing by medieval
standards. As an example, we have a rare instance of mathematics being used as a tool of
diplomacy. Frederick felt obligated to participate in the Crusades, but instead of attacking Jerusalem
with his superior force he set up camp outside and patiently worked out a peaceful
takeover. Frederick and Sultan al-Kamil arranged what we might call cultural exchanges to ease
tensions as the negotiations proceeded, and at one point a list of mathematical problems was sent to
the Arabic scholars of Jerusalem as a friendly challenge [p. 217]. Click here for more information on
Frederick's crusade. Click here for a picture of some of Frederick's remaining castles. Click here for
more biographical information on Frederick.

Leonardo was clearly delighted by the spirit present at Frederick's court. His book Liber abbaci was
dedicated to Michael Scott, Frederick's closest advisor on scientific matters [pp. 306-7]. Two other
scholars associated with Frederick, John of Palermo and Master Theodore, appear in The Book of
Squares. In fact, the book begins with Leonardo's explanation of how a question from John prompted
his research, and an answer to a question from Theodore brings the book to a close. The initial
challenge from John of Palermo was this:

1/4 find a square number from which, when five is added or subtracted, always arises a square
number [p. 3].

In modern notation this means finding x, y, and z so that

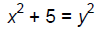and

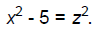
This is easy enough if you allow irrational solutions, for instance taking x = Ö17, y = Ö22, and z =
Ö12. But further reading makes it clear that Leonardo is looking for a rational solution (it is not hard
to see that a solution in integers is impossible). His work then leads him to consider many more
questions about sums and differences of squares .

First Steps

How can we find two squares that sum to a square? Leonardo answers this question in several ways,
with the first method following from a simple observation that provides inspiration throughout the
book:

I thought about the origin of all square numbers and discovered that they arise out of the increasing
sequence of odd numbers; for the unity is a square and from it is made the first square, namely 1; to
this unity is added 3, making the second square, namely 4, with root 2; if to the sum is added the third
odd number, namely 5, the third square is created, namely 9, with root 3; and thus sums of
consecutive odd numbers and a sequence of squares arise together in order [p. 4].

Thus, the sums 1 + 3 + 5 + 7 = 16 and 1 + 3 + 5 + 7 + 9 = 25 are both squares. Since we add the
square 9 to the first sum in order to get the second, we have16 + 9 = 25 as a sum of two squares
adding to a third square. Leonardo explains that we could use any odd square in place of 9 to do the
same thing. For instance, using 49, we have 1 + 3 +1/4+ 47 = 576 and 1 + 3 +1/4+ 49 = 625, so 576 +
49 = 625 is another sum of the same form. Leonardo goes on to note that the final two or more terms
of these odd-number sums can also sum to a square. For instance, an even square can be
partitioned into consecutive odd numbers, an example being 17 + 19 = 36. Since 1 + 3 +1/4+ 15 = 64
and 1 + 3 +1/4+ 19 = 100, we get 64 + 36 = 100.

Taking things further, Leonardo poses the following:

I wish to find three squares so that the sum of the first and the second as well as all three numbers
are square numbers [p. 105]

He explains his solution this way:

I shall find first two square numbers which have sum a square number and which are relatively prime.
Let there be given 9 and 16, which have sum 25, a square number. I shall take the square which is
the sum of all odd numbers which are less than 25, namely the square 144, for which the root is the
mean between the extremes of the same odd numbers, namely 1 and 23. From the sum of 144 and
25 results, in fact, 169, which is a square number. And thus is found three square numbers for which
the sums of the first two and all three together are square numbers [p. 105].

In fact, Leonardo points out that this method can be extended to any number of squares, since (1 + 3
+ 1/4 + 167) + 169 = 7056 + 169 = 84^2 + 13^2 = 85^2 = 7225, and (1 + 3 + 1/4 + 7223) + 7225 = 3612^2 +
85^2 = 3613^2. Thus, we get the following sequence of squares:

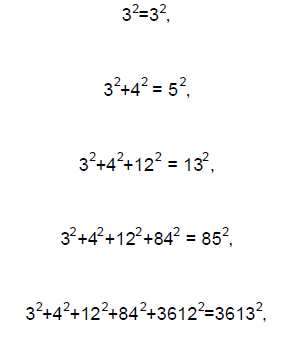
Congruous Numbers

The solution to John of Palermo's problem requires several steps and some of the most intricate work
in The Book of Squares. The first step seems at first to be unrelated:

If two numbers are relatively prime and have an even sum, and if the triple product of the two
numbers and their sum is multiplied by the number by which the greater number exceeds the smaller
number, there results a number which will be a multiple of twenty-four [p. 48].

Leonardo often represents numbers as lengths. Here he considers points a, b, and g on a line , with
the two numbers being the lengths from a to b and from b to g. Thus, in our notation, the expression
under discussion is

ab · bg ·( ab + bg )·( bg - ab ),

assuming that ab and bg are relatively prime with bg > ab. Leonardo proves it is a multiple of 24 by
carefully checking cases. He calls the numbers obtained from this kind of product congruous.

The purpose of the congruous numbers is shown a little later while addressing the following problem:
Find a number which added to a square number and subtracted from a square number yields always
a square number [p. 53].

This is John of Palermo's problem except it does not require the number to be 5. Let us continue
using ab and bg as before. We throw in the additional condition that bg·(bg-ab) < ab·(ab+bg), which
will keep us in the realm of positive integers in what follows. Leonardo's method involves the bg·(bgab)
consecutive odd numbers centered at ab·(ab + bg) and also the ab·(bg - ab) consecutive odd
numbers centered at bg·(ab + bg). In the example given in the book, ab = 3 and bg = 5, so we get 10
consecutive odd numbers centered at 24:

15, 17, 19, 21, 23, 25, 27, 29, 31, 33,

and also 6 consecutive odd numbers centered at 40:

35, 37, 39, 41, 43, 45.

These two sequences have an amazing relationship. They are next to each other in the list of all odd
numbers, and they have the same sum, 240, which is the congruous number ab·bg·(ab + bg)·(bg -
ab) = 3·5 ·8 ·2. Thus,

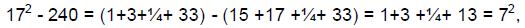
and

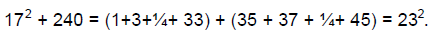
This solves the problem. Now, how can Leonardo use this idea with 5 instead of 240?

The Solution

Leonardo realizes that what he needs is a congruous number that is 5 times a square , because then
he can divide through by that square and leave just the 5 [p. 76]. The values ab = 4 and bg = 5
almost work, since 4·5 ·(4+5) ·(5-4) = 180 = 5 ·6^2. But 4+5 is not even as is required for a congruous
number, the problem being that there are not 5 consecutive odd numbers centered at 36, or 4
centered at 45. Leonardo gets around this by doubling all the values. There are 10 consecutive odd
numbers centered at 72, namely those from 63 to 81. There are also 8 consecutive odd numbers
centered at 90, those from 83 to 97. Both sequences sum to 720=5·12^2, and we get

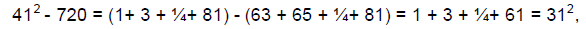
and

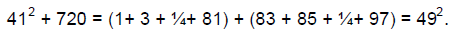
Finally, Leonardo has his answer. He writes

There is for the first square 6 97/144, with root 2 7/12, which results from dividing 31 by the root of
144, which is 12, and there is for the second, which is the sought square, 11 97/144, with root 3 5/12,
which results from dividing 41 by 12, and there is for the last square 16 97/144 with root 4 1/12 [p.78].

In modern notation, we could write

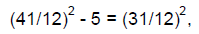
and

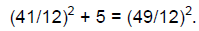
Questions for Investigation

1. Find all the ways to express 225 as a sum of consecutive odd integers. Use your results to find
the squares that can be added to 225 to produce another square. What determines the number of
ways in which a given number can be expressed as a sum of consecutive odd numbers?

2. Show that 336 is a congruous number. Use your results to find a rational number x such that x^2 –
21 and x^2 + 21 are both squares of rational numbers. Can you find examples with numbers other
than 5 (shown in the text) and 21?

3. There is a correspondence between ordered triples (a,b,c) with a^2 + b^2 = c^2 and ordered triples
(p,q,r) with p^2, q^2, r^2 forming an arithmetic progression. The triple (a,b,c) = (3,4,5) corresponds to
(p,q,r) = (1,5,7), the triple (a,b,c) = (5,12,13) corresponds to (p,q,r) = (7,13,17), and the triple (a,b,c) =
(8,15,17) corresponds to (p, q, r) = (7,17,23).
Discover the rule for this correspondence and explain why it works.

4. Triangular numbers can be found by the taking the sum of all integers from 1 to n , so we get 1 =
1, 1 + 2 = 3, 1 + 2 + 3 = 6, 1 + 2 + 3 + 4= 10, and so on. Adapt as many of Leonardo’s results as you
can to the case of triangular numbers.