Solving Equations Using Exponents and Logarithms

Theorem 1.1. The Change of Base Formula If we wished to find log₇ 300,
we know that 7² = 49, and that 7³ = 343, so log₇ 300 is between two and three.
We can narrow this guess down by using rational exponents, but we cannot “plug
it in” to a calculator , since there is no “log₇” key. We need a change of base
formula:

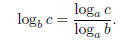
That is, we take the log (with any base) of the original mantissa, the number
we are taking the log of , and divide it by the log (with the same base) of the
original base. In our example, this gives

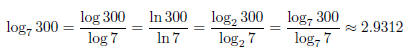
Remark 1.2. Our toolbox of solving equations now contains two powerful tools:
the fact that logarithms and exponentials are inverse functions, and this change
of base formula. Let us see what we can do with them.

Example 1.3. Consider the equation e^{ln x} = 5. Solve for x.
Soln: Since raising “e” to a power and taking the natural log are inverse
functions, when we compose them, we get x back:
e^{ln x} = x.

Then x = 5. This is, indeed, in our domain (the domain of logarithms is the
positive reals ), so we are finished.

Example 1.4. Consider the equation e^{ln x} = −5. Solve for x.
Soln: Since raising “e” to a power and taking the natural log are inverse
functions, when we compose them, we get x back:
e^{ln x} = x.

Then x = −5. This cannot be, however, since −5 is not in the domain of ln x.
That is, ln (−5) does not exist. So we throw it away. This equation must have
no solution.

Example 1.5. Consider the equation ln (ln x) = 4. Solve for x.
Soln: Use the fact that ln x is the inverse function of e^x to get rid of one of
the ln’s: Raise “e” to the power of each side of the equation, and we have

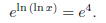
As inverse functions, one of these cancel, leaving
ln x = e⁴.

To rid ourselves of the remaining natural log, we may again raise “e” to the
power of each side:

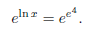
The left side cancels again, leaving

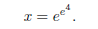
Although not pretty, 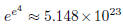is certainly positive, and in our domain.
Thus, we are finished.

Example 1.6. Consider the equation e^3x+2 = 1. Solve for x.
Soln1: Notice that 1 = e⁰. Then e^3x+2 = e⁰ implies that 3x + 2 = 0. This
gives that x = −2/3 . Since the domain of e^x is all reals, we are finished.

Soln2: Using the inverse (logarithmic) function, we have that
ln e^3x+2 = ln 1

Then the ln and the power of “e” cancel, leaving
3x + 2 = ln 1 = 0,

at which point we return to the first solution.

Example 1.7. Consider the equation 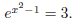.Solve for x.
Soln: There is no slick trick that we can employ on this one, since 3 is not
a power of “e.” Therefore, we must resort to the inverse trick:

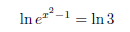
This gives us
x² − 1 = ln 3.

For now, we will leave ln 3 in the equation, and continue to solve:

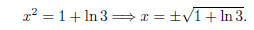
Since ln 3 > 0, the radicand is positive, and in our domain. Thus,

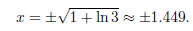
Example 1.8. Consider the equation e^2x− 4e^x + 4 = 0. Solve for x.
Soln: Hidden in this equation, there is a quadratic. Notice that (e^x)² = e^2x.
So our equation becomes
(e^x)² − 4e^x + 4 = 0
(e^x − 2)² = 0
e^x − 2 = 0
e^x = 2

Then, making use of our logarithmic form,
x = ln 2.

Example 1.9. Consider the equation log₇ x − log₇ (1 − x) = 4. Solve for x.
Soln: Using properties of logarithms, we see the difference of the logs is the
log of the quotient:

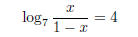
By definition of log, we switch to exponential form:

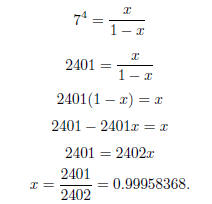
This is in our domain, so we are finished.

Example 1.10. Consider the equation log₁₃ (x² − 3x + 15) = 1. Solve for x.
Soln: Using the “log roll,” or setting this equation back in exponential form,
we see that
13¹ = 13 = x² − 3x + 15
0 = x² − 3x + 2

Then by hook, by crook, by completing the square, by quadratic formula, or by
factoring, we get that x = 1 or x = 2. Since both of these are in our domain,
we have our solutions.

Example 1.11. Consider the equation log₂ 3x + log₂ 4x = log₂ 12. Solve for x.
Soln: Using the properties of logs, we see that the sum of logs is the log of
the product :
log₂ 3x · 4x = log₂ 12
log₂ 12x² = log₂ 12

Similarly to how we solved exponential equations; namely, that if the bases were
equal, and the results were equal, the exponents must have been equal; we have
that two logs are equal and have the same base. Therefore, their mantissas
(stuff inside the log) must be the same:
12x² = 12 => x² = 1 => x = ±1.

However, if we use −1 for x, we get a negative value inside the logarithm in our
original equation. Therefore, we throw it out. The positive x value is valid, so
x = 1.

Example 1.12. Consider the equation 4^x+3 = 5^7-3x. Solve for x.
Soln: In this case, we will not be so lucky as to have things cancel out, since
four and five are not the same base. How do we choose which logarithm to use?!
Since things will not cancel anyway, it does not matter. All that matters is that
we get the x’s down from the exponent. We will use the natural log here, we
used the common log (base 10) in class. You can use whatever log you like.
ln 4^x+3 = ln 5^7-3x

Using properties of logs , we can pull the exponents out in front:
(x + 3) ln 4 = (7 − 3x) ln 5

To get x on one side, and everything else on the other, we will have to distribute.
Treat the logarithm like any other number, say a square root , or π , so that you
don’t drag it too far.
x ln 4 + 3 ln 4 = 7 ln 5 − 3x ln 5

Bringing all x’s to one side and everything else to the other yields
x ln 4 + 3x ln 5 = 7 ln 5 − 3 ln 4
x(ln 4 + 3 ln 5) = 7 ln 5 − 3 ln 4

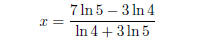
Now, this is a completely acceptable answer. However, to get used to the properties
of logs, we will simplify.
Bring all powers inside the log:

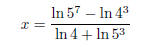
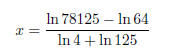
Use that the difference of logs is the log of the quotient and that the sum of the
logs is the log of the product:

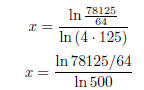
Which, if we really want to be special, can be simplified by the change of base
formula:

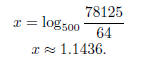
Example 1.13. Consider the equation 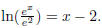Solve for x.
Soln: By the properties of exponents, we have that
ln e^x-2 = x − 2.

Since ln x and e^x are inverse functions, we get that
x − 2 = x − 2,

which is true for every x. Thus, our solution set is all real numbers.

Example 1.14. Consider the function 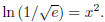Solve for x.
Soln: By the properties of exponents, we have that

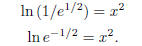
Since ln x and e^x are inverse functions, we get that
−1/2 = x².

This is impossible. Thus, we have no real solution for our equation.

Remark 1.15. Homework for the sections on logarithms will be the following:
• From 6.1 on exponents, problems 11 − 17, 21, 25, 31, 33, 35, 36
• From 6.2 on Euler’s constant, problems 1 − 5, 8, 12, 15 − 22
• From 6.3 on logs, problems 7, 9, 13, 15, 21, 30, 32, 34, 36.
• From 6.4 on the properties of logs, problems 3, 5, 7, 15, 63
• From 6.5 on solving equations, problems 1, 3, 5, 25, 35, 36, 37

There are 49 problems listed. Although it would behoove you to work all of them
in preparation of the test , only 25 will be turned in. Choose at least 4 problems
from each section, and the last 5 are your choice. This homework will be due
on Wednesday, 22 March.