Complex Numbers
I. Definitions
A. The number i.
1.
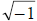 = i
= i
2. So i2 = -1
B. Complex Numbers
1. A complex number is any number of the form a + bi, where a and b are
real
numbers.
2. Examples
a. –5 + 2i
b. 7 + 2/3i
c. 5i = 0 = + 5i
d. -15 = -15 + 0i
3. So you can see that the real numbers are a subset of the complex numbers.
4. This also will enable us to find the square root of a negative number.
5. a + bi is called the standard form of a complex number.
II. Addition and Subtraction
A. Procedure
1. Combine like terms .
2. Put in standard form.
B. Examples - Simplify each of the following .
1. (8 + 9i) + (5 - 6i) - (4 - 3i)
First, we will distribute to get rid of the parentheses :
8 + 9i + 5 - 6i - 4 + 3i
Combining the like terms, we get:
Answer: 9 + 6i
2. Now you try one: (3 + 2i) - (0 + 5i) - (5 + 4i)
Answer: -2 - 7i
III. Multiplication
A. Procedure
1. Use the Distributive Property
2. Combine like terms
3. Use the fact that i2 = -1
4. Put the answer in standard form
B. Examples - Perform the indicated Multiplication
1. (3 + i)(3 - i)
Using the Distributive Property, we get:
9 - 3i + 3i - i2
Combining like terms and remembering that i2 = -1, we have:
9 - (-1)
OR
Answer: 10
2. (6 + 3i)(4 + 3i)
Using the Distributive Property, we get:
24 + 18i + 12i + 9i2
Combining like terms and remembering that i2 = -1, we have:
24 + 30i + 9(-1)
OR
24 + 30i - 9
OR
Answer: 15 + 30i
3. Now you try one: (4 - i)(2 - i)
Answer: 7 - 6i
IV. Division of Complex Numbers
A. Procedure
1. Multiply the numerator and denominator by the conjugate of the denominator.
2. Simplify.
3. Write in Standard Form
B. Examples - Perform the indicated Division.
1.
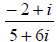
The conjugate of the denominator is 5 - 6i, so multiplying numerator and
denominator by that, we get:
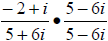
Using the Distributive Property in both the numerator and denominator, we
get:
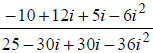
Combining like terms and using the fact that i2 = -1, we get:
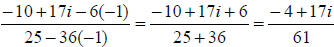
Writing in standard form, we get:
Answer:
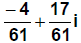
2.
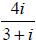
The conjugate of the denominator is 3 - i, so we multiply numerator and
denominator by that to get:
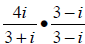
Using the Distributive Property, we get:
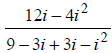
Combining like terms and using the fact that i2 = -1, we get:
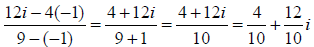
Reducing , we get:
Answer:
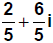
3. Now you try one:
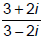
Answer:
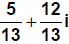
V. Square Roots of Negative Numbers
A. Now that we have defined i, we can take a perfect square out of every
negative
square root, namely the square root of -1.
B. Note that all other perfect squares are the same.
C. Examples - Simplify each Square Root
1.
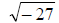
We notice that 9 will go evenly into 27, so that's a perfect square we can take
out, and -1 is also a perfect square that we can take out, leaving 3 behind. So
it will look like:
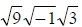
OR
Answer:
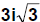
2.
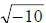
The only perfect square that we can take out of this one is -1. So we have:
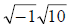
Answer: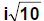
3.
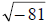
81 is a perfect square, so is -1. So we have:
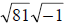
Taking the square roots, we get:
Answer: 9i
4. Now you try one:
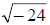
Answer: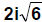
VI. Powers of i
A. Recall that anything to the zero power is equal to 1. We will use this
fact to generate
a table of powers of i.
B. Powers of i
1. i0 = 1
2. i1 = i (When we multiply both sides by i.)
3. i2 = -1 (When we multiply both sides by i and use the definition.)
4. i3 = -i (When we multiply both sides by i.)
5. i4 = -i2 = - (-1) = 1 (When we multiply both sides by i and use the
definition.)
6. i5 = i (When we multiply both sides by i.)
7. i6 = i2 = -1 (When we multiply both sides by i and use the definition.)
8. i-7 = -i (When we multiply both sides by i.)
9. i8 = -i2 = 1 (When we multiply both sides by i and use the definition.)
10. Notice that we have a pattern! There are, in reality, only 4 possible values
for
i to a power . So recapping what we have:
11.
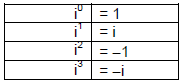
12. So how will we use this to find, say i343? We will divide the exponent by
4, but
really what we are interested in is the remainder.
a. If the remainder is 0, our answer is 1.
b. If the remainder is 1, our answer is i.
c. If the remainder is 2, our answer is −1.
d. If the remainder is 3, our answer is −i.
C. Examples - Simplify each expression.
1. i343
First, we divide 343 by 4. We get 85.75. So what we really have is 85 R 3.
This means that we can write the expression as :
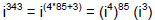 (Using rules of exponents )
(Using rules of exponents )
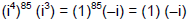
Answer: −i
So in the future, we will only be concerned with the
remainder. On the
calculator , if there is no decimal, the remainder is 0. If you have .25, the
remainder is 1. If you have .5, the remainder is 2. If you have .75, the
remainder is 3.
2.
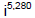
Dividing 5,280 by 4, we get no remainder.
Answer: 1
3. Now you try one:
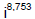
Answer: i
| Prev | Next |