Continued Fractions and the Euclidean Algorithm
5 The symbol 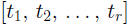
For arbitrary real numbers 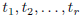 with each
with each
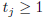 for j ≥ 2 the symbol
for j ≥ 2 the symbol
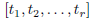
is defined recursively by:
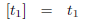
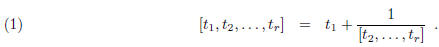
In order for this definition to make sense one needs to know that the
denominator in the
right -hand side of (1) is non-zero. The condition
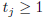 for j ≥ 2 guarantees, in fact, that
for j ≥ 2 guarantees, in fact, that
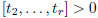 , as one may prove using induction.
, as one may prove using induction.
It is an easy consequence of mathematical induction that the symbol
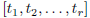 is a rational
is a rational
number if each 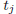 is rational. In particular,
each finite continued fraction is a rational number .
is rational. In particular,
each finite continued fraction is a rational number .
(Note that the symbol 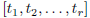 is to be called a
continued fraction, according to the
is to be called a
continued fraction, according to the
convention of the first section, only when each
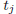 is an integer.)
is an integer.)
Observe that the recursive nature of the symbol
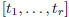 suggests that the symbol should
suggests that the symbol should
be computed in a particular case working from right to left. Consider again, for
example, the
computation above showing that [2, 3, 5, 2] = 81/35. Working from right to left
one has:
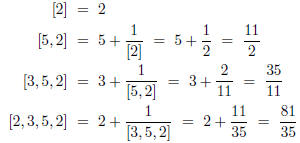
There is, however, another approach to computing
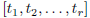 . Let, in fact,
. Let, in fact,
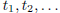 be
be
any (finite or infinite) sequence of real numbers. One uses the double recursion
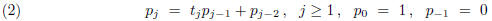
to define the sequence ![]() , j ≥ − 1. The double recursion, differently
initialized ,
, j ≥ − 1. The double recursion, differently
initialized ,
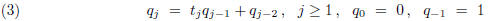
defines the sequence 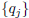 , j ≥ − 1. Note
that
, j ≥ − 1. Note
that 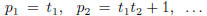 and
and 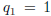 ,
,
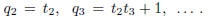
One now forms the matrix
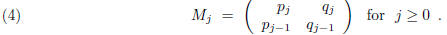
Thus, for example,
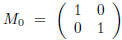 and
and
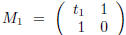
It is easy to see that the matrices 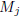 satisfy
the double recursion
satisfy
the double recursion
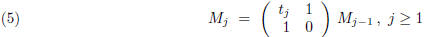
as a consequence of the double recursion formulas for the
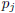 and
and 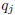 .
Hence, a simple argument
.
Hence, a simple argument
by mathematical induction shows that
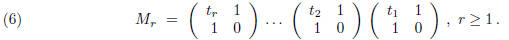
This is summarized by :
Proposition 1. For any sequence 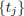 , j ≥
1 of real numbers, if
, j ≥
1 of real numbers, if 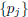 and
and
![]() are the
are the
sequences defined by the double recursions (2) and (3), then one has the matrix
identity
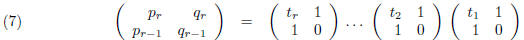
for each integer r ≥1.
Corollary 1. One has the identity 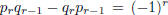 for
each integer r ≥1.
for
each integer r ≥1.
Proof. The number 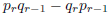 is the determinant of the
matrix
is the determinant of the
matrix ![]() . From the formula
. From the formula
(6) the matrix 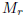 is the product of r matrix
factors , each of which has determinant −1. Since
is the product of r matrix
factors , each of which has determinant −1. Since
the determinant of the product of matrices is the product of the determinants of
the factors, it
is clear that 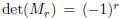 .
.
Corollary 2. One has the vector identity
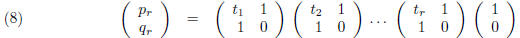
for each integer r ≥1.
Proof. First recall (i) that the product of a matrix and a (column) vector is
defined by the
relation
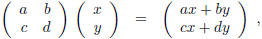
(ii) that the transpose of a matrix is the matrix whose
rows are the columns of the given matrix,
and (iii) that the transpose operation reverses matrix multiplication. One
tranposes both sides
of the relation (7) to obtain:
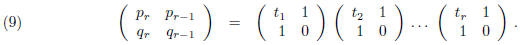
To this relation one applies the principle that the first
column of any 2×2 matrix is the product
of that matrix with the column
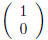
in order to obtain the column identity (8).
Theorem 2. For any sequence
![]() , j ≥ 1 of real numbers,
if
, j ≥ 1 of real numbers,
if ![]() and
and
![]() are the sequences
are the sequences
defined by the double recursions (2) and (3), and if
![]() for j ≥ 2, then
the value of the
for j ≥ 2, then
the value of the
symbol ![]() is given by
the formula
is given by
the formula
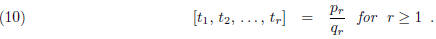
Proof. What is slightly strange about this important
result is that while the  and the
and the
 are defined by the front end recursions,
albeit double recursions, (2) and (3), the symbol
are defined by the front end recursions,
albeit double recursions, (2) and (3), the symbol
![]() is defined by the
back end recursion (1). The proof begins with the comment that
is defined by the
back end recursion (1). The proof begins with the comment that
the right-hand side of (10) does not make sense unless one can be sure that the
denominator
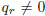 . One can show easily by induction on r that
. One can show easily by induction on r that
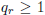 for r ≥1 under the hypothesis
for r ≥1 under the hypothesis
![]() for j ≥ 2.
for j ≥ 2.
The proof proceeds by induction on r. If r = 1, the assertion of the theorem is
simply the
statement 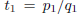 , and, as noted above,
, and, as noted above,
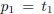 and
and 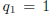 .
Assume now that r ≥ 2.
.
Assume now that r ≥ 2.
By induction we may assume the correctness of the statement (10) for symbols of
length r − 1,
and, therefore, for the symbol 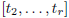 . That case of
the statement says that
. That case of
the statement says that 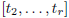
must be equal to a/c , where by corollary 2
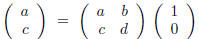
with
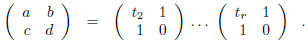
Now by (1)
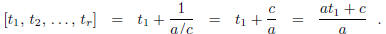
But by corollary 2 again
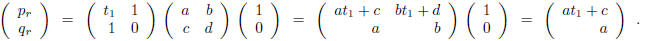
Hence,
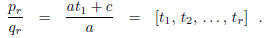
6 Application to Continued Fractions
Recall that 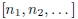 is called a continued fraction
only when each
is called a continued fraction
only when each ![]() is an
integer and
is an
integer and
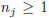 for j ≥ 2. The sequence
for j ≥ 2. The sequence
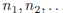 may be finite or infinite. The symbol
may be finite or infinite. The symbol
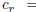
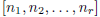 formed with the first r terms of the sequence , is called the rth convergent of
the
formed with the first r terms of the sequence , is called the rth convergent of
the
continued fraction. Associated with a given sequence
![]() are two sequences
are two sequences
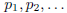
and 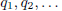 that are given, according to the double recursions (2), (3) of
the previous section
that are given, according to the double recursions (2), (3) of
the previous section
with 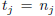 .
.
Proposition 2. If
![]() is a continued fraction, then the integers
is a continued fraction, then the integers
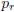 and
and 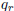 are coprime
are coprime
for each r ≥1.
Proof. By Corollary 1 of the previous section
![]() . Hence,
any positive
. Hence,
any positive
divisor of both 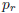 and
and 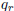 must divide the left-hand side of this relation, and,
therefore, must
must divide the left-hand side of this relation, and,
therefore, must
also divide (−1)r.
Proposition 3. The difference between successive convergents
of the continued fraction
![]()
is given by the formula
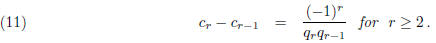
Proof. According to the theorem (formula 10) at the end of
the last section the convergent 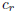
is given by
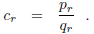
Hence,
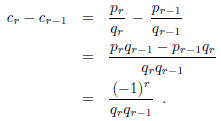
(The last step is by Corollary 1 above.)
Remark 1. The formula (11) remains true if
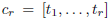 where the
where the
![]() are real numbers
are real numbers
subject to the assumption
![]() for j ≥1.
for j ≥1.
Lemma. The sequence ![]() is a strictly increasing sequence for j ≥ 2.
is a strictly increasing sequence for j ≥ 2.
Proof. This is easily proved by induction from the recursive definition (3) of
the sequence.
Theorem 3. If ![]() is an infinite continued fraction, then the limit
is an infinite continued fraction, then the limit
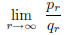
always exists.
Proof. As one plots the convergents
![]() on the line of real numbers, one moves
alternately right
on the line of real numbers, one moves
alternately right
and left. The formula (11) for the difference between successive convergents
elucidates not only
the fact of alternate right and left movement but also the fact that each
successive movement
is smaller than the one preceding. Therefore, one has
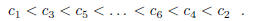
Since any strictly increasing sequence of positive integers must have infinite
limit, the seqence
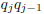 has infinite limit, and so the sequence of
reciprocals
has infinite limit, and so the sequence of
reciprocals 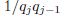 must
converge to zero .
must
converge to zero .
Hence, the sequences of odd- and even-indexed convergents must have the same
limit, which is
the limit of the sequence of all convergents.
Definition 1. The limit of the sequence of convergents of an infinite continued
fraction is called
the value of that continued fraction.
Theorem 4. If
![]() is the continued fraction
expansion of an irrational number x, then
is the continued fraction
expansion of an irrational number x, then
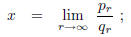
that is, the value of the continued fraction expansion of a real number is that
real number.
Proof. For each r ≥1 the continued fraction expansion
![]() of x is
characterized by
of x is
characterized by
the identity

where 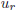 is a real number with
is a real number with
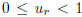 . The sequences of p’s and q’s for the
symbol
. The sequences of p’s and q’s for the
symbol
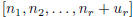 agree with those for the symbol
agree with those for the symbol
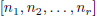 except for the rth terms.
except for the rth terms.
One has by (10)
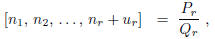
where by (3)
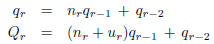
Hence,
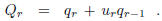
Therefore, the displacement from 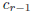 to x is by (11)
to x is by (11)
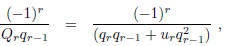
which is in the same direction but of smaller magnitude than the displacement
from 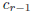 to
to
![]() . Therefore, x must be larger than every odd-indexed convergent and smaller
than every
. Therefore, x must be larger than every odd-indexed convergent and smaller
than every
even-indexed convergent. But since all convergents have the same limit, that
limit must be x.
| Prev | Next |