Real Zeros of Polynomial Functions

In the previous sections , we covered a method for factoring a polynomial
by testing potential zeros with synthetic division to see if the remainder is
zero. One problem: There is an infinite number of "potential" zeros to
test.

The Rational Zero Test narrows down the list of potential
rational zeros to check.

Example: Find the rational zeros of f(x) = x^4- x^3 -8x + 8
.
According to the Rational Zero Test, all rational zeros will have the form
x = p/q where p is a factor of 8 and q is a factor of 1 .

p is one of the following: {1,-1, 2, -2 , 4, -4, 8, -8}
q is one of the following: {1, -1}

The possibilities of p /q include:
1/1 = 1, 1/-1 = -1, -1/1 = -1, -1/-1 = 1, 2/-1 = -2, -2/-2 = 1,
4/1 = 4, 4/-1 = -4, -4/1 = -4, -4/-1 = 4, 8/1=8, 8/-1 = -8, -8/1 = -8, -8/-1 = 8
 

As you have probably noticed, many possibilities are repeated.
The list of possibilities is summarized as {+/-1, +/-2, +/-4, +/-8}.

These 8 are POSSIBLE rational zeros. To see which, if any, are actual zeros,
you must check with synthetic division .

Synthetic division using these 8 possible zeros reveals that 2 of them are zeros
and the other 6 are not. x = 1 and x = 2 are zeros. The synthetic division for
these 2 values is given below

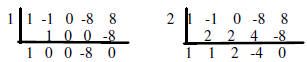
Notes on The Rational Zero Test

The Rational Zero Test only finds potential RATIONAL zeros. A rational zero
is a zero that may be written as a positive or negative whole number, a fraction,
a terminating decimal ( like 0.25), or a repeating decimal that represents a
fraction (like 0.3333. . . =1/3). This test DOESN'T indicate possible
IRRATIONAL zeros. An irrational zero is a zero that is a complex number
(like 3 + 2i) or a decimal that does not terminate or repeat with a pattern.
x= sqrt(2) = 1.414213566237. . .is irrational. So is (1 +sqrt(3))/2.

For example, f(x) = x^2+ x + 1 has possible rational zeros of 1 and -1, but
neither are zeros. In this case, both zeros are irrational. In fact, they are
complex numbers.

Completely Factoring a Polynomial

We may use the rational zero test and the idea that the factorization
is written in terms of zeros to completely factor f(x) = x^4-x^3- 8x +8.

Previously in this section, we found the possible rational zeros to be
x = +/-1, +/-2, +/-4, and +/-8. Testing these resulted in only x = 1 and x = 2
as actual zeros.

This means that f(x) = (x - 1)(x - 2)( unknown quadratic factor ). Thus, we
know that x^4 - x^3 - 8x + 8 = (x - 1)(x - 2)( unknown quadratic factor).

Since (x-1)(x-2) = x^2 - 3x + 2, we may also say that

x^4 - x^3 -8x + 8 =(x^2 -3x +2)(unknown quadratic factor).

We may long divide f(x) by x^2-3x +2 in order to find that quadratic factor.
This division is shown on the next page.
Note that we can't use synthetic division when dividing by a quadratic.
 

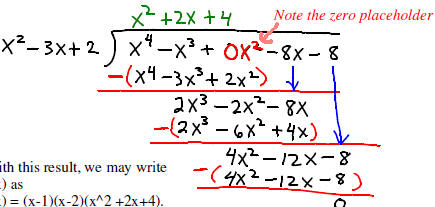
With this result, we may write
f(x) as
f(x) = (x-1)(x-2)(x^2 +2x+4).
To completely factor f(x), we must find the zeros of the quadratic x^2 +2x +4
by using the quadratic formula.

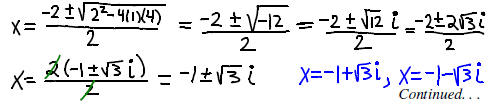
Since the 4 zeros of x^4 -x^3- 8x + 8 are

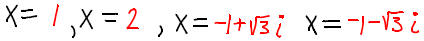
the factorization is

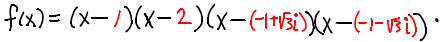
We may remove the extra parentheses and write this as

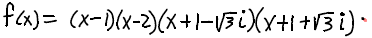
Can I do This Problem Without Long Dividing?

The answer is YES. Another, different approach to factoring
f(x) = x^4 - x^3 - 8x + 8, uses synthetic division instead of long
polynomial division . The difference in this method is that we reduce
the polynomial as we check the possible zero with synthetic division.

See the next page. . . .

Another Approach to Factoring x^4 -x^3 -8x+8

We start checking the possible rational zeros +/-1,+/-2,+/-4, +/-8.

We start with x = 1. Using synthetic division, we obtain

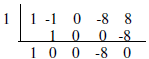
The bottom row indicates the coefficients of
the result after dividing.

The result after dividing is 1x^3 +0x^2+0x - 8 or x^3 - 8.

At this point we know that f(x) = (x-1)(x^3 - 8).

Now, check for zeros in x^3 - 8. Checking x=2 with synthetic division
results in
 
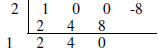
This means that x^3 - 8 = (x - 2) (x^2 + 2x + 4) Continued. . .

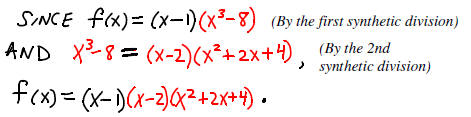
We may finish the factorization by finding the zeros of the quadratic
x^2+2x + 4 with the quadratic formula, as was done using the first method .

In this method, we "break down" f(x) into a linear factor multiplied by another
polynomial of lesser degree. We then break down that polynomial of lesser
degree by finding its zeros and factoring it. When we obtain a quadratic, we
may break it down by factoring it directly or using the quadratic formula to
find its zeros.

Descartes Rule of Signs & Bound Rules for Real Zeros
You are not responsible for this. These rules are important in a Senior-level
college math course for Math majors but may be excluded in this course.
Do the assigned homework for 3.4. Read the text!