Unit Fractions
A unit fraction is a fraction of the form 1/n, where n is
a positive integer . In this problem, you
will find out how rational numbers can be expressed as sums of these unit
fractions. Even if you
do not solve a problem , you may apply its result to later problems.
We say we decompose a rational number q into unit
fractions if we write q as a sum of 2 or
more distinct unit fractions. In particular, if we write q as a sum of k
distinct unit fractions, we
say we have decomposed q into k fractions. As an example, we can decompose 2/3
into 3 fractions:
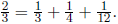
1. (a) Decompose 1 into unit fractions.
Answer:
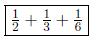
(b) Decompose 1/4 into unit fractions.
Answer:
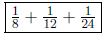
(c) Decompose 2/5 into unit fractions.
Answer:
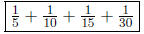
2. Explain how any unit fraction 1/n can be decomposed into other unit fractions.
Answer:

3. (a) Write 1 as a sum of 4 distinct unit fractions.
Answer:
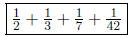
(b) Write 1 as a sum of 5 distinct unit fractions.
Answer:
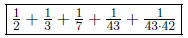
(c) Show that, for any integer k > 3, 1 can be decomposed
into k unit fractions.
Solution : If we can do it for k fractions, simply replace the last one
(say 1/n) with
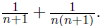 Then we can do it for k +1 fractions. So,
since we can do it for k = 3, we
Then we can do it for k +1 fractions. So,
since we can do it for k = 3, we
can do it for any k > 3.
4. Say that a/b is a positive rational number in simplest
form, with a ≠ 1. Further, say that n is
an integer such that:
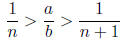
Show that when 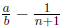 is
written in simplest form, its numerator is smaller than a.
is
written in simplest form, its numerator is smaller than a.
Solution: 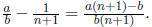 Therefore,
when we write it in simplest form, its numerator
Therefore,
when we write it in simplest form, its numerator
will be at most a(n + 1) − b. We claim that a(n + 1) − b < a. Indeed, this is
the same as
an − b < 0 <-> an < b <-> b/a > n, which is given.
5. An aside: the sum of all the unit fractions
It is possible to show that, given any real M , there exists a positive integer k
large enough
that:
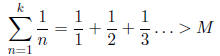
Note that this statement means that the infinite harmonic series,
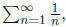 grows without
grows without
bound, or diverges. For the specific example M = 5, find a value of k, not
necessarily the
smallest, such that the inequality holds . Justify your answer.
Solution: Note that
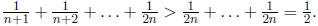 Therefore,
if we apply this
Therefore,
if we apply this
to n = 1, 2, 4, 8, 16, 32, 64, 128, we get
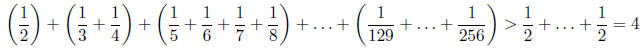
so, adding in 1/1 , we get
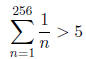
so k = 256 will suffice.
6. Now, using information from problems 4 and 5, prove that the following
method to decompose
any positive rational number will always terminate:
Step 1. Start with the fraction a/b . Let t1 be the largest unit fraction 1/n
which is less than or
equal to a/b .
Step 2. If we have already chosen t1 through tk,
and if t1 +t2 +. . .+tk is still less than a/b
, then
let tk+1 be the largest unit fraction less than both tk
and a/b .
Step 3. If t1 + . . . + tk+1 equals a/b , the decomposition is found. Otherwise, repeat step 2
Why does this method never result in an infinite sequence of ti?
Solution: Let 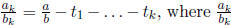 is a fraction in simplest terms. Initially, this
is a fraction in simplest terms. Initially, this
algorithm will have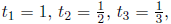 etc. until
etc. until
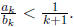 This will eventually happen
This will eventually happen
by problem 5, since there exists a k such that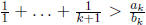 At
that point, there is
At
that point, there is
some n with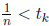 such that
such that
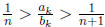 In this case,
In this case,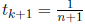
Suppose that there exists nk such that
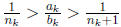 for some k. Then we have
for some k. Then we have
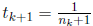
and 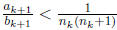 This shows that once we have found nk
such that
This shows that once we have found nk
such that 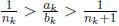 and
and
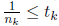 we no longer have to worry about tk+1
being less than tk, since
we no longer have to worry about tk+1
being less than tk, since 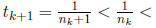
tk, and also 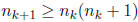 while
while
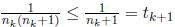
On the other hand, once we have found such an nk,
the sequence {ak} must be decreasing
by problem 4. Since the ak are all integers, we eventually have to
get to 0 (as there is no
infinite decreasing sequence of positive integers). Therefore, after some finite
number of steps
the algorithm terminates with 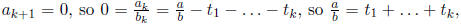
which is what we wanted.
Juicy Numbers [100]
A juicy number is an integer j > 1 for which there is a
sequence a1 < a2 < . . . < ak of positive
integers such that ak = j and such that the sum of the reciprocals of
all the ai is 1. For example,
6 is a juicy number because 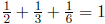 , but 2 is not
juicy.
, but 2 is not
juicy.
In this part, you will investigate some of the properties
of juicy numbers. Remember that if
you do not solve a question, you can still use its result on later questions.
1. Explain why 4 is not a juicy number.
Solution: If 4 were juicy, then we would have
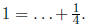 The . . . can only possible contain
The . . . can only possible contain
1/2 and 1/3 , but it is clear that 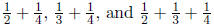 are all
not equal to 1.
are all
not equal to 1.
2. It turns out that 6 is the smallest juicy integer. Find
the next two smallest juicy numbers,
and show a decomposition of 1 into unit fractions for each of these numbers. You
do not need
to prove that no smaller numbers are juicy.
Answer:
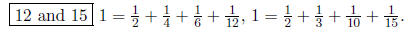
3. Let p be a prime. Given a sequence of positive integers
b1 through bn, exactly one of which
is divisible by p , show that when
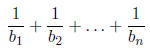
is written as a fraction in lowest terms , then its
denominator is divisible by p. Use this fact
to explain why no prime p is ever juicy.
Solution: We can assume that bn is the
term divisible by p (i.e. bn = kp) since the order
of addition doesn’t matter. We can then write
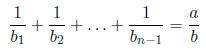
where b is not divisible by p (since none of the bi
are). But then 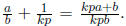 Since b
Since b
is not divisible by p, kpa + b is not divisible by p, so we cannot remove the
factor of p from
the denominator. In particular, p cannot be juicy as 1 can be written as 1/1 ,
which has a
denominator not divisible by p, whereas being juicy means we have a sum
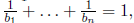
where  and so in particular none of the bi
with i < n are divisible by
p.
and so in particular none of the bi
with i < n are divisible by
p.
4. Show that if j is a juicy integer, then 2j is juicy as
well.
Solution: Just replace
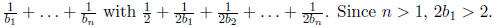
5. Prove that the product of two juicy numbers (not
necessarily distinct) is always a juicy
number. Hint: if j1 and j2 are the two numbers, how can
you change the decompositions of
1 ending in 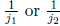 to make them end in
to make them end in
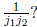
Solution: Let 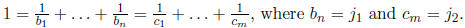 Then
Then
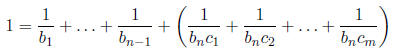
and so j1j2 is juicy.
| Prev | Next |