Competency Requirements for Mathematics

UNIT 7: BASIC ALGEBRA

The student demonstrate competency in the following tasks with a minimum of 80%
accuracy.

7.1

The student shall demonstrate ability to accurately calculate an answer to a formula involving the process of evaluating the expression .

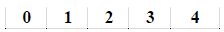Example: A = 2(x + y) -1 for x = 2, y = 4

7.2

The student shall demonstrate ability to simplify algebraic expressions by adding and subtracting terms.

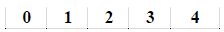Example: Simplify by adding and subtracting terms.

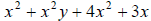
7.3

The student shall demonstrate ability to solve one variable linear equations involving practical problem applications.

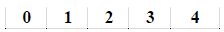Example: D = RT is used to calculate the distance D traveled by an
object moving at a constant average speed R during an elapsed time
T. How long would it take a pilot to fly 1240 miles at an average
speed of 220 mph?

1240 = 220T
5.6 = T or 5 hours 35 minutes

7.4

The student will demonstrate the process of solving two -step equations involving practical problems.

Example: A repair service charges $ 45.00 for a house call and an
additional $36.00 per hour for repair work. The formula T = 45 +
36H represents the total charge T for H hours of work. If the total
bill for a customer was $225.00, how many hours of actual labor was
there?

220 = 45 + 36H

4.8 = H or 4 hours 48 minutes

7.5

The student will demonstrate the process of solving an equation with variables .

Example: 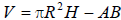solve for H

7.6

The student shall demonstrate the ability to accurately translate simple English sentences and phrases into mathematical expressions or equations.

Example: Horsepower required to overcome air resistance is equal to
the cube of the vehicle speed in miles per hour multiplied by the
frontal area in square feet divided by 150,000.

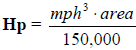
7.7

The student shall demonstrate the ability to divide and multiply algebraic expressions .

Examples: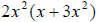

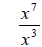
7.8

The student shall demonstrate the ability to accurately convert large and small numbers into a Scientific Notation.

Example: 93,000,000 = 9.3×10⁷

Example: .0000456 = 4.56 ×10^-5

8.1

The student shall demonstrate the ability to name, classify, and measure angles including practical problems.

Example: In the pipe flange the six bolts are equally spaced, what is
the spacing of the holes in degrees?

8.2

The student shall demonstrate ability to accurately calculate area and perimeter of given polygons.

Example: A large rectangular window measures 72 5/8 in by 60 3/8
in. Calculate the area of this opening. Round to the nearest square
inch.

8.3

The student shall demonstrate the ability to accurately classify types of triangles, calculate area, and determine missing measurements of triangles.

Example: Calculate the missing measurement using the Pythagorean
Theorem, and area of the right triangle.

8.4

The student shall demonstrate the ability to accurately calculate side length, distance across the corners, and cross sectional area of a hexagon.

Example: In machine trades a hexagonal nut measures ¾ inch across
the flats, find the side length, distance across the corners, and cross
sectional area. Students will round answers to three significant digits .

8.5

The student shall demonstrate ability to accurately determine circumference and area of circles and partial circles.

Example: If a hole is cut using a ¾ inch diameter wood bit, what will
be the radius and circumference of the hole?

Example: Find the area of stained glass used in a semicircular
window with a radius of 9 inches.

Note to student: To receive credit you must provide documentation of competency
achievement. Copies of your unit or final exams may be used to document competency
achievement and serve to supplement your instructors report of competency.

Granting of college credit requires you have received a grade of A or B for the articulated
course, provided documentation of competency attainment AND you have submitted
required admissions and registrations forms.