Least Common Multiples
a) Finding the Least Common Multiple
The Least Common Multiple of two natural numbers→ is the smallest common multiple of both.
Example 1 page 232
L.C.M 20 and 30; Getting the L.C.M. through the lists
20: 40 (20∙2), 60 (20∙3), 80, 120, 140, 160, 180, 200, 240
30: 60 (30∙2), 90 (30∙3), 120, 150, 180, 210, 240, 270
Common Multiples: 60, 120, 180, 240 → The Least Common Multiple is 60.
Finding the Least Common Multiples through Prime Factorization
Through this method we use prime factorization and
divisibility rules .
Example: Find the L.C.M. of 8 and 10
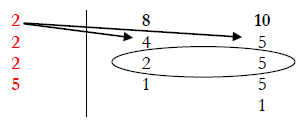
Start in order (Remember the prime factorization list: 2, 3, 5, 7, 11, 13, 17) and find if any of the two numbers is divisible by that prime number. Then, divide, as the arrows show, and place your quotient under the numbers. However, if the number only works with one of the numbers like in the case of 2 and 5, rewrite the number that you don’t use and continue with the prime # list until you find a number that works. Finally, your goal is to get both numbers to 1.
Finding the L.C.M. of numbers and variables
Example 11 page 236: Find the L.C.M. of
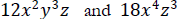
First, find the L.C.M. of the numbers, 12 and 18. The L.C.M is 36
Second, identify your variables. In this case we have x, y and z. Now compare their exponents and choose the highest exponent value. This value is your L.C.M for the value. However, if you have nothing to compare it to just rewrite that variable and exponent as your L.C.M.
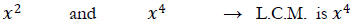
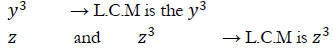
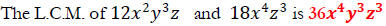
4.2 Addition, Order and Applications
To add fractions with like denominators:
- Add the numerators.
- Keep the same denominator.
- Simplify the result , if possible.
Exercise 3 page 240
b) Additions using the Least Common Denominator or L .C.D.
When we have two different denominators we must find the L.C.M. of the denominators, we call this the Least Common Denominator or L.C.D.
Example:
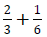
- First, find the L.C.D of 3 and 6. L.C.D = 6
- Second, transform each fraction to an equivalent fraction with a denominator
of 6. Like so,

- Third, use the new equivalent fractions and add the numerators since they have the same denominator.
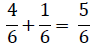
Example 10 page 240
c) Order of Fractions
When the denominators are different , we cannot compare fractions to see which one is bigger. Thus, we need to find the L.C.D. in order to compare both fractions. Remember that to indicate order we use the < , “greater than” or >, “less than” symbols .
Example:

Find, the L.C.D of 6 and 8. The L.C.D is 24
Find equivalent fractions
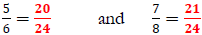
Compare,
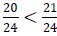
| Prev | Next |