Decimals and Fractions
4. Write the following decimals as fractions in simplest form .

5. Consider the fraction
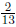 .
.
(a) Without dividing, explain how you know this fraction can be expressed as a
repeating decimal.
Since 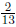 is a rational number we know that it
can be expressed as either a terminating decimal or a
is a rational number we know that it
can be expressed as either a terminating decimal or a
repeating decimal. This will be a repeating decimal since the denominator has
prime factors other than
2’s and 5’s.
(b) Before actually finding the decimal, determine what
the longest the repetend could be? Explain carefully.
We know it will start repeating once a remainder is repeated. Since it is not a
terminating decimal we
can never get remainder 0, therefore the only remainders we could possibly get
when dividing by 13 are
1,2,3,4,5,6,7,8,9,10,11 and 12. Thus after at the most 12 steps of long division
one of the remainders
must repeat. In other words, the repetend can be at most 12 digits long .
(c) Express 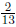 as a decimal. Be sure to show
all your steps.
as a decimal. Be sure to show
all your steps.

Since we get the remainder 2 again, we know this will
start repeating now. Therefore 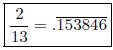
11.
(a)
Max asks, ”Why do we have to line up the decimal when we are adding but not when
we are multiplying?”
How do you respond to Max?
Remember when adding fractions we had to get a common denominator . In other
words, when adding
we have to add the same size pieces. By lining up the decimal we are adding
digits in the same place
value, so we are guaranteeing that we are adding the same size pieces. However,
remember when
multiplying fractions we did not need to get a common denominator, so when
multiplying decimals we
do not need to line up the decimal.
(b)
He then asks, ”Will I get the wrong answer if I line up the decimals when
multiplying?” How do you
respond to Max?
As long as you still count the number of digits behind the decimal point and
place it correctly in the
product you will get the correct answer even if you originally line up the
decimal points.
12.
(a) Give your students a step by step guide on how to subtract two decimals .
Step 1: Line up the decimal points.
Step 2: Place zeros in empty spaces to right of decimal if needed.
Step 3: Add as if they were whole numbers and bring the decimal point directly
down into the answer.
(b) Do the problem 25.6 − 4.712.
(c) Use the above example to show why the algorithm you gave in part 0a works.
With subtraction of integers we are always just subtracting in each place value
and we use the exchange
rate of 10 to 1 if needed. This does not change to the right of the decimal
point, we still subtract in
each place value and the exchange rate is still 10 to 1. So lining up the
decimal just insures that we are
subtracting the same place values.
13. (a) Give your students a step by step guide on how to multiply two decimals.
Step 1: Multiply as if they are whole numbers.
Step 2: Count how many digits are to the right of the decimal in each factor .
Step 3: In the product, count over from the right to the left the total number
you got in Step 2 and
place the decimal point there.
(b) Do the problem 23.4 × 2.568.
(c) Use the above example to show why the algorithm you gave in part 0a works.
Step 1: Multiply as if they are whole numbers.
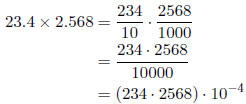
The part in parenthesis corresponds to multiply as if they
were whole numbers and the 10−4 part
corresponds to moving the decimal left four places.
14.
(a) Give your students a step by step guide on how to divide a whole number into
a decimal.
Step 1: Place decimal right above where it started.
Step 2: Divide as if they are whole numbers.
Step 3: If you do not get remainder zero, keep adding zeros to the dividend
until you get remainder
zero or a repeating pattern.
(b) Do the problem 54.18 ÷ 5.
(c)
Use the above example to show why the algorithm you gave in part 0a works.
Just with addition and subtraction, we do division place value by place value.
So it does not matter if
we are to the right of the decimal point or not. Lining up the decimal just
insures that we are keeping
the same place values.
15.
(a) Give your students a step by step guide on how to divide a decimal into a
decimal.
Step 1: Move the decimal point to the end of the divisor. Then move the decimal
that same amount to
the right in the dividend.
Step 2: Proceed as in example (c).
(b) Do the problem 54.18 ÷ 2.5.
(c) Use the above example to show why the algorithm you gave in part 0a works.
We have already justified step 2 in problem (c). So we need only justify why we
can move the decimal.
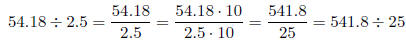
So moving the decimal the same amount in both numbers,
simply corresponds to the fundamental law
of fractions (with multiplier 10 in this case).
| Prev | Next |