Design of Line Algorithms
Basic Math Review
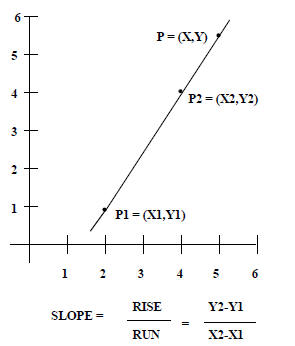
Slope- Intercept Formula For Lines
Given a third point on the line:
P = (X,Y)
Slope = (Y - Y1)/(X - X1)
= (Y2 - Y1)/(X2 - X1)
Solve for Y
Y = [(Y2-Y1)/(X2-X1)]X
+ [-(Y2-Y1)/(X2-X1)]X1 + Y1
or
Y = mx + b
Other Helpful Formulas
Length of line segment between P1 and P2:
L = ¦ [ (X2-X1)2 + (Y2-Y1)2 ]
Midpoint of a line segment between P1 and P3:
P2 = ( (X1+X3)/2 , (Y1+Y3)/2 )
Two lines are perpendicular iff:
M1 = -1/M2
Parametric Form of the Equation
of a 2D Line
Given points P1 = (X1, Y1) and P2 = (X2, Y2)
X = X1 + t(X2-X1)
Y = Y1 + t(Y2-Y1)
When
t = 0 we get (X1,Y1)
t = 1 we get (X2,Y2)
As 0 < t < 1, we get all points between (X1,Y1) and (X2,Y2)
Basic Line Algorithm
Must:
1. Compute integer coordinates of pixels which lie on or near a line.
2. Be efficient.
3. Create visually satisfactory images.
• Lines should appear straight
• Lines should terminate accurately
• Lines should have constant density
• Line density should be independent of line length and angle
4. Always be defined.
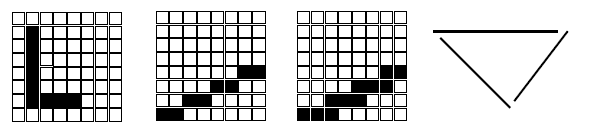
Simple DDA Line Algorithm
{Based on the parametric equation of a line }
| Procedure DDA(X1,Y1,X2,Y2 :Integer); Var Length, I :Integer; X,Y,Xinc,Yinc : Real ; Begin |
For I := 0 To Length Do Begin Plot(Round(X), Round(Y)); X := X + Xinc; Y := Y + Yinc End {For} End; {DDA} |
Creates good lines, but problems ...
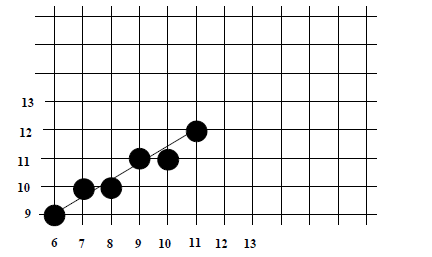
DDA Example
Render the line from (6,9) to (11,12):
Length := Max of (ABS(11-6), ABS(12-9)) = 5
Xinc := 1
Yinc := 0.6
Values computed are:
(6,9),
(7,9.6),
(8,10.2),
(9,10.8),
(10,11.4),
(11,12)
Fast Lines Using The Midpoint Method
Assumptions: line between points (0,0) and (a,b) with
Recall: y = mx + B (m is the slope, B is the y-intercept)
=>m = b/a and B = 0
=>y = (b/a)x + 0
=>f(x,y) = bx - ay = 0
Two choices for next pixel (T or S),
want the pixel closer to line!
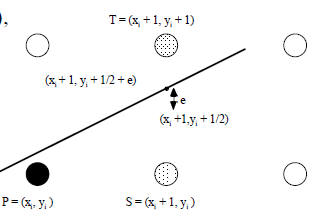
Assume distance between
pixel centers is 1
Midpoint is (xi + 1,yi + 1/2)
e is difference between midpoint and where line crosses between
S and T
If e is positive , line crosses above the midpoint and is closer to T
If e is negative , line crosses below the midpoint and is closer to S
=> don’t need exact value of e
Fast Lines - The Decision Variable
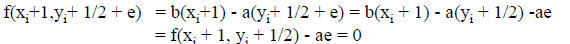
Let
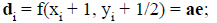 di is known as the decision variable.
di is known as the decision variable.
Since a ≥ 0, di has the same sign as e.
Algorithm:
If di ≥ 0 then
Choose T = (xi + 1, yi + 1) as next point
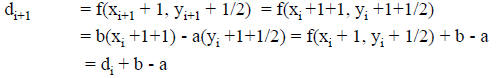
else
Choose S = (xi + 1, yi) as next point
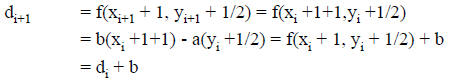
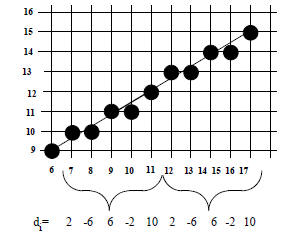
Fast Line Algorithm
Calculate initial value for d0 directly from f(x,y) at (0,0):
d0 = f(0 + 1, 0 + 1/2) = b(1) - a(1/2) = b - a/2
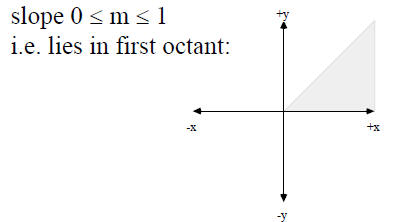
Algorithm for a line from (0,0) to (a,b) in the first octant is:
| x := 0; y := 0; d := b - a/2; For i := 0 to a do Begin Plot(x,y); If d ≥ 0 Then Begin x := x + 1; y := y + 1; d := d + b - a End |
Else Begin x := x + 1; d := d + b End End |
The only non-integer value is a/2
How can we get rid of it?
Bresenham’s Line Algorithm
Generalize for lines beginning at points other than (0,0)
| Begin {Bresenham for lines with slope between 0 and 1} a := ABS(xend - xstart); b := ABS(yend - ystart); d := 2*b - a; Incr1 := 2*(b-a); Incr2 := 2*b; If xstart > xend Then Begin x := xend; y := yend End Else Begin x := xstart; y := ystart End; |
For I := 0 to a Do Begin Plot(x,y); x := x + 1; If d ≥ 0 Then Begin y := y + 1; d := d + incr1 End Else d := d + incr2 End {For Loop} End; {Bresenham} |
Optimizations
Detect cycles in the decision variable
=>correspond to a repeated pattern of pixel choices
Save pattern, reuse if a cycle is detected
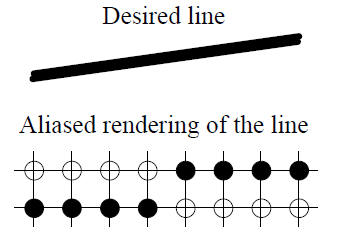
Antialiasing
Aliasing caused by finite addressability of CRT
Approximation of lines with discrete points can result in a
staircase appearance or "Jaggies"
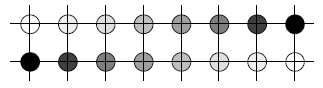
Antialiasing - Solutions
Aliasing can be smoothed out by using higher addressability.
Problem: addressability usually fixed
Solution: intensity is variable, so use it
=> two adjacent pixels can give impression of point part way
between
=> perceived location of point dependent upon ratio of
intensities
An antialiased line has virtual pixels “located” at the proper
addresses
Antialiased Bresenham Lines
Use the distance (e = di/a) value to determine pixel intensities.
Three possible cases for the Bresenham algorithm:
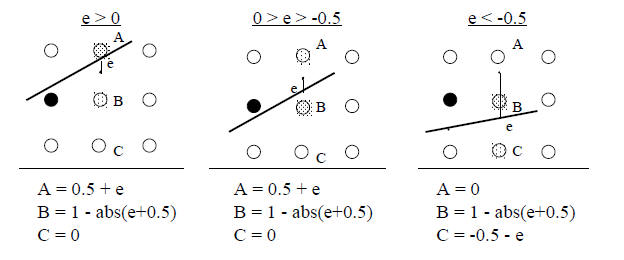
What about color?
| Prev | Next |