Distance and Midipoint Formula; Circle
Objectives:
1. To find the distance between two points
2. To find the midpoint of a line segment
3. To write the standard form of a circle’s equation
4. To give the center and radius of a circle whose
equation is in standard form
5. To convert the general form of a circle’s equation to
standard form
Objective 1: To find the distance between two points
The distance Formula
Given two points P1(x1,y1) and P2(x2,y2)
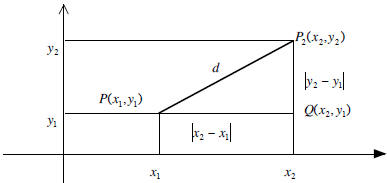
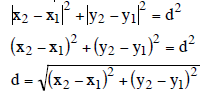
Example: Find the distance between (-4, -1) and (2, - 3).
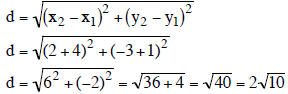
Objective 2: To find the midpoint of a line segment
Finding the midpoint
Formula :
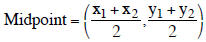
Find the midpoint of the line segment with endpoints
(-4,-1) and (2, - 3)
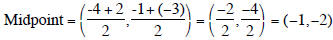
Objective 3: To write the standard form of a circle’s
equation
Circle:
A circle is the set of all points in a plane that are
equidistant from a fixed point called the center. The fixed
distance from the circle’s center is called the radius.
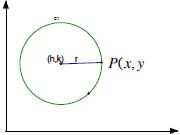
Find the formula of a circle whose center is (h, k) and
radius is r.
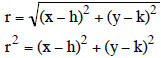
The equation of a circle whose center is at the origin and
radius r is x2 + y2 = r2.
Write the standard form of the equation of the circle with
center at (0,0) and the radius is 4. Graph the circle on the
board.
Equation: x2 + y2 = 16.
Write the standard form of the equation of a circle with
center (-2, 1) and radius 2. Graph circle on the board.
Equation:
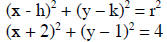
Objective 4: To give the center and radius of a circle
whose equation is in standard form
Give the center and radius of a circle whose equation is
(x + 4)2 + (y + 5)2 = 36.
The center is (-4,-5) and the radius is 6.
Objective 5:
To convert the general form of a circle’s equation to
standard form
The general form of the equation of a circle is
x2 + y2 Dx + Ey + F= 0
Standard Form: (x - h)2 + (y – k)2 = r2
Express x2 + y2 +8x + 4y + 16= 0 in standard form and
find the center and the radius.
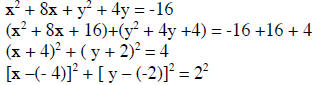
Center: (-4,-2) and radius = 2
Express x2 + y2 - 6y - 7= 0 in standard form and find the
center and the radius.
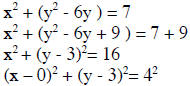
Center: (0, 3) and radius is 4
| Prev | Next |