Exponents and Radicals
Radicals and Properties of Radicals
Radicals (or roots) are, in effect, the opposite of exponents. In other
words, the nth root of a number a is a
number b such that
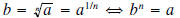
The number b is called an nth root of a. The number n is referred to as the
index of the radical (if no index
appears, n is understood to be 2). The principal nth root of a number is the nth
root of a which has the same
sign as a . For example both 2 and - 2 satisfy 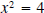 , but 2 is the (principal)
square root of 4.
, but 2 is the (principal)
square root of 4.
Examples:
• 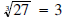 since
since
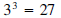
•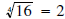 since
since
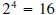 (Note
(Note 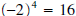 also, but 2 is the principal 4th root
also, but 2 is the principal 4th root
•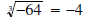 since
since
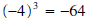
•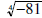 is not a real number and we will say that it does not exist. (In this
course we won’t learn how to
is not a real number and we will say that it does not exist. (In this
course we won’t learn how to
take an eventh power of a negative number .)
Radicals are used to define rational exponents :
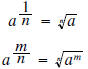
The notation 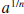 is extremely useful, and we encourage you to use it whenever
you have to simplify
is extremely useful, and we encourage you to use it whenever
you have to simplify
expressions involving radicals.
Examples:
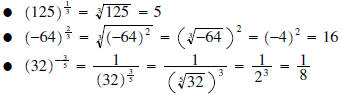
Since radicals are nothing more than rational exponents ,
many of the properties of exponents also apply to
radicals.
| Property | Example |
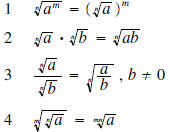 5a If n is odd 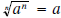 5b If n is even 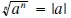 |
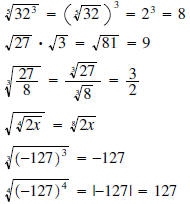 |
The following list is a restatement of these properties,
but in exponential notation . You need to be familiar
with both radical and exponential notation, and be able to convert between the
two.
| Property | Example |
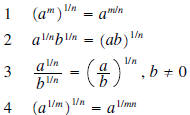 5a If n is odd 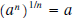 5b If n is even 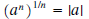 |
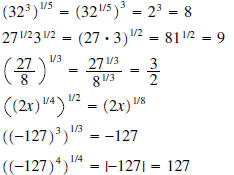 |
Examples:
• 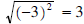 (refer to Property 5b)
(refer to Property 5b)
• 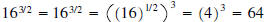 (refer to property 1-given the right hand
side)
(refer to property 1-given the right hand
side)
• 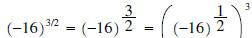 (refer to property
1)
(refer to property
1)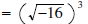
There is no answer as we cannot take the square root of -16.
•
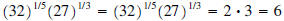
| Prev | Next |