GCF and LCM
BASIC ALGEBRA
TOPIC 2 – REVIEW FOR EXAM
The exam covers concepts learned in Lessons 2.1, 2.2, 2.3 and 2.4. The following objectives were introduced:
1. Identify constants, variables, terms and coefficients
in an algebraic expression
2. Combine like terms
3. Evaluate expressions and formulas for given values of the variables
4. Recognize a linear equation
5. Solve a linear equation with whole number coefficients
6. Solve an equation with fractional coefficients
7. Solve equations with no solutions or infinite solutions
8. Solve formulas for a particular variable
9. Translate words into algebraic expressions
10. Solve word problems
11. Recognize solutions of linear inequalities
12. Graph solutions of inequalities in one variable
13. Solve a linear inequality
14. Solve problems involving inequalities
To study for the exam:
1. review material on the CD
2. in your PAN for each lesson (2.1, 2.2, 2.3, 2.4)
• review objectives (pages 136, 160, 179, 198)
• read the EXPLAIN sections and do the sample problems for EXPLAIN and EXPLORE
(pages 127-135, 141-159, 165-178, 187-197)
• do the HOMEWORK (pages 137, 161, 180-181, 199)
• review the APPLY practice problems you have done
• do the EVALUATE practice test (pages 139, 164, 185, 201) (note: answers to all
questions for the EVALUATE practice test may be found at the back of your PAN)
3. do the Topic 2 Cumulative Activities in your PAN (pages 202-203)
Also review: GCF and LCM
Adding and Subtracting Fractions
Basic Algebra Review -- 2.1-2.4
1. Identify: 11 + 4y – 6 + 2x – 1
a) constants
b) terms
c) coefficients
d) variables
Simplify the expressions :
2. 2x – 5 + 4y + 3x – 7y + 4
3. 5 + 3(x – 1)
4. 3(y – 4) + 4y(x + 2) + 5
5. 7(2 – x) – 8 – 2(y – 3x) + 4y
Evaluate the expressions:
6. 4x – 7 when x = -3
7. 2x + 3y + 5 when x = 2 and y = 1
8. 3xy – 2x + 1 – y when x = -1 and y = 2
9. xy^2 – 4y + 2 – 3x when x = 3 and y = -2
Solve for each variable:
10. x + 15 = 37
11. 9t = 108
12. –7 = w + 29
13. 2x + 3 = 17
14.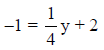
15. 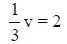
16. 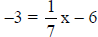
17. 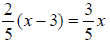
18. 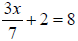
19. 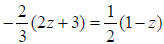
20. 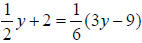
21. 4(w + 1) – 3w = w + 4
22. 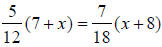
23. Solve for z: 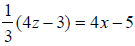
24. Solve for r: C = 2πr
25. Solve for a: 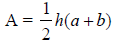
Solve the following word problems:
26. The sum of two numbers is 39. The smaller number plus
twice the larger number
is 62. What are the two numbers?
27. A 90 cm pipe is cut into two pieces so that one piece
is 6 cm shorter than the other.
Find the length of each piece.
28. True or False? The number 5 is a solution of the inequality y + 3 > 8.
29. Graph x ≤ -2 on the given number line:
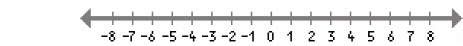
30. Solve for x and graph the solution set on the number line: 3x + 4 ≥ 1
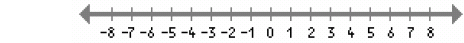
31. Solve for x and graph the solution set on the number line: -8x – 20 < 4
32. Solve for x and graph solution set on the number line: -4 ≤ 2x + 2 < 10

33. The sum of two numbers is less than 64. One of the numbers is 23.
a) Write an inequality for the above statement.
b) What are the possible solutions for the other number?
Answer Key:
1. a) 11, -1, -6
b) 11, 4y, -6, 2x, -1
c) 11, 4, -6, 2, -1
d) x, y
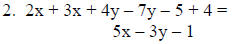
3. 5 + 3x – 3 = 3x + 2
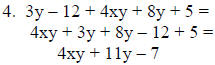
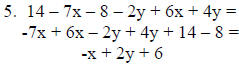
6. 4(-3) – 7 = -12 – 7 = -19
7. 2(2) + 3(1) + 5 = 4 + 3 + 5 = 12
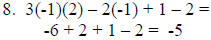
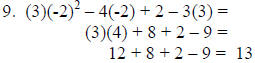
10. x = 22
11. t = 12
12. w = -36
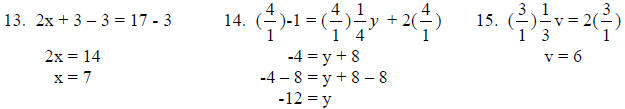
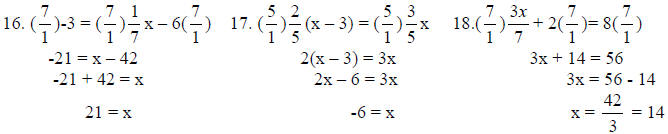
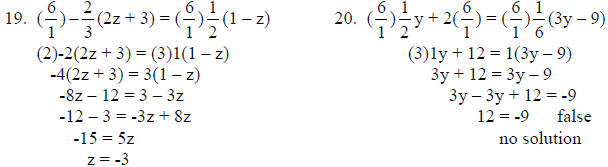
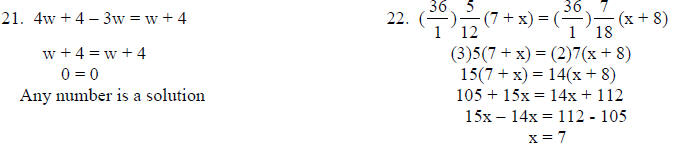

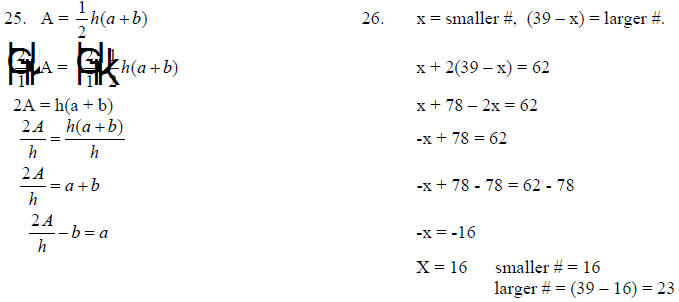
27. x = longer piece, x – 6 = shorter piece
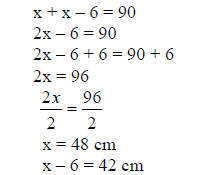
28. False
29. x ≤ -2
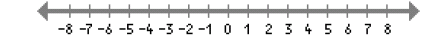
30. 3x + 4 ≥ 1;
3x ≥ -3;
x ≥ -1
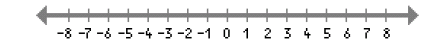
31. -8x – 20 < 4
-8x < 24 ;
x > -3
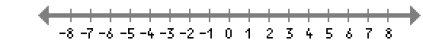
32. -4 ≤ 2x + 2 < 10
-6 ≤ 2x < 8 ;
-3 ≤ x < 4
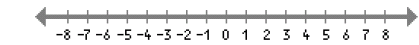
33. a) x + 23 < 64
b) x < 41
| Prev | Next |