Introduction to Analytic Number Theory
Chapter 0
Primes and the Fundamental
Theorem of Arithmetic
Primes constitute the holy grail of analytic number theory, and many of
the famous theorems and problems in number theory are statements about
primes. Analytic number theory provides some powerful tools to study prime
numbers, and most of our current (still rather limited) knowledge of primes
has been obtained using these tools.
In this chapter, we give a precise definition of the concept of a prime,
and we state the Fundamental Theorem of Arithmetic, which says that every
integer greater than 1 has a unique (up to order) representation as a product
of primes. We conclude the chapter by proving the infinitude of primes.
The material presented in this chapter belongs to elementary (rather
than analytic) number theory, but we include it here in order to make the
course as self-contained as possible.
0.1 Divisibility and primes
In order to define the concept of a prime, we first need to define the notion
of divisibility.
Given two integers d ≠ 0 and n, we say that d divides n or n is
divisible by d, if there exists an integer m such that n = dm. We write
d l n if d divides n, and 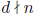 if d does not
divide n.
if d does not
divide n.
Note that divisibility by 0 is not defined, but the integer n in the above
definition may be 0 (in which case n is divisible by any non-zero integer d)
or negative (in which case d l n is equivalent to d l (-n)).
While the above definition allows for the number d in the relation "d l n"
to be negative, it is clear that d l n if and only if (-d) l n, so there is a
one-to-one
correspondence between the positive and negative divisors of an integer
n. In particular, no information is lost by focusing on the positive divisors
of a given integer, and it will be convenient to restrict the notion of a
divisor
to that of a positive divisor. We therefore make the following convention:
Unless otherwise specified, by a divisor of an integer we mean a positive
divisor, and in a notation like d l n the variable d represents a positive
divisor
of n. This convention allows us, for example, to write the sum-of-divisors
function σ (n) (defined as the sum of all positive divisors of n) simply as
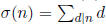 , without having to add the extra condition d
> 0 under the
, without having to add the extra condition d
> 0 under the
summation symbol .
The greatest common divisor (gcd) of two integers a and b that are
not both zero is the unique integer d > 0 satisfying (i) d l a and d l b, and
(ii)
if c l a and c l b, then c l d. The gcd of a and b is denoted by (a, b). If (a,
b) = 1,
then a and b are said to be relatively prime or coprime.
The least common multiple (lcm) of two non-zero integers a and b
is the unique integer m > 0 satisfying (i) a l m and b l m, and (ii) if a l n
and
b l n, then m l n. The lcm of a and b is denoted by [a, b].
The gcd and the lcm of more than two integers are defined in an analogous
manner.
An integer n > 1 is called prime (or a prime number) if its only
positive divisors are the trivial ones, namely 1 and n.
The sequence of primes, according to this ( commonly accepted ) definition
is thus 2, 3, 5, 7, 11,... Note, in particular, that 1 is not a prime, nor is
0 or any negative integer.
Primes in other algebraic structures. The notion of a "prime" can
be defined in quite general algebraic structures. All that is needed for such
a definition to make sense is an analog of the multiplication operation (so
that divisibility can be defined), and the notion of "units" (which serve as
"trivial" divisors, analogous to the numbers ±1 among the integers). One
can then define a prime as any element in the given structure that can only
be factored in a trivial way, in the sense that one of the factors is a unit.
The
best-known examples of such structures are algebraic integers, which behave
in many respects like the ordinary integers, and which form the subject of
a separate branch of number theory, algebraic number theory.
Another example is given by the ring of polynomials with integer coef-
ficients, with multiplication of ordinary polynomials as ring operation and
the constant polynomials ±1 as "units". The "primes" in such a polynomial
ring turn out to be the irreducible (over Z) polynomials.
0.2 The Fundamental Theorem of Arithmetic
As the name suggests, this result, which we now state, is of fundamental
importance in number theory, and many of the results in later chapters
depend in a crucial way on this theorem and would fail if the theorem were
false.
Theorem 0.1 (Fundamental Theorem of Arithmetic). Every integer
n > 1 can be written as a product of primes , and the representation is unique
up to the order of the factors.
The proof of this result, while elementary, is somewhat involved, and we
will not give it here. (It can be found in any text on elementary number
theory.) We only note here that the crux of the proof lies in showing the
uniqueness of a prime factorization, the proof of the existence of such a
factorization is an easy exercise in induction.
Notation. There are several common ways to denote the prime factorization
guaranteed by the Fundamental Theorem of Arithmetic. First, we can
write the prime factorization of an integer n ≥ 2 as
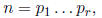
where the pi's are primes, but not necessarily distinct.
In most situations it is more useful to combine identical factors in the
above representation and write
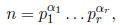
where, this time, the pi's are distinct primes, and the exponents
![]() positive
positive
integers.
Using the notation 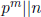 if pm is the exact power
of p that divides n
if pm is the exact power
of p that divides n
(i.e., pm l n, but
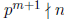 ),
we can write the above representation as
),
we can write the above representation as
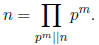
Yet another useful representation of the prime factorization of n is
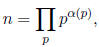
where the product is extended over all prime numbers and
the exponents
α(p) are nonnegative integers with α(p) ≠ 0 for at most finitely many p.
The last notation is particularly convenient when working with the greatest
common divisor or the least common multiple, since these concepts have
a simple description in terms of this notation: Indeed, if n and m are positive
integers with prime factorization 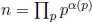 and
and
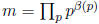 , then
, then
the gcd and lcm of n and m are given by
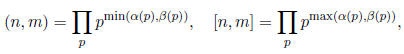
respectively. Similarly, divisibility is easily
characterized in terms of the exponents
arising in the representation: Given 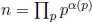 and
and
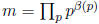 ,
,
we have m l n if and only if β(p) ≤ α(p) for all p.
With the convention that an empty product is to be interpreted as 1, all
of the above formulas remain valid when n = 1.
Unique factorization in more general algebraic structures. As
mentioned above, the concept of a prime can be defined in very general
algebraic structures. One can then ask if an analog of the Fundamental
Theorem of Arithmetic also holds in these structures. It turns out that the
existence part of this result, i.e., the assertion that every (non-unit) element
in the given structure has a representation as a product of "prime" elements,
remains valid under very general conditions. By contrast, the uniqueness
of such a representation (up to the order of the factors or multiplication by
units) is no longer guaranteed and can fail, even in some simple examples.
For instance, in the ring of algebraic integers
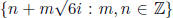 , the
, the
number 10 can be factored as 10 = 2 · 5 and 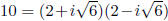 , and one
, and one
can show that each of the four factors 2, 5, 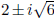 arising here are "primes"
arising here are "primes"
in the appropriate sense.
Beurling generalized primes. By the Fundamental Theorem of Arithmetic
the positive integers are exactly the products of the form ( * )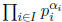 ,
,
where 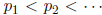 is the sequence of primes, I a finite (possibly empty)
is the sequence of primes, I a finite (possibly empty)
subset of the positive integers, and the exponents
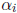 are positive integers.
are positive integers.
This characterization of the positive integers suggests the following
generalization
of the concepts of a "prime" and a (positive) "integer", which was
first proposed some 50 years ago by Arne Beurling. Instead of starting with
an appropriate analog of the integers and then trying to define a notion of a
prime, the idea of Beurling was to start with an
appropriate generalization
of the primes and then define generalized integers as above in terms of these
generalized primes. Specifically, let 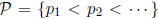 be an arbitrary
be an arbitrary
sequence of positive numbers (which need not even be integers), and let 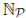
be the set of all finite products of the form ( *) with the pi's taken from P.
Then P is called a system of Beurling generalized primes, and
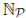 the associated
the associated
system of Beurling generalized integers. One can study such systems
in great generality, and ask, for instance, how the "growth" of such a sequence
of generalized primes is related with that of the associated sequence
of generalized integers.
| Prev | Next |