Linear Algebra
1. Let

a) Row reduce to put A in echelon form.
b) Continue row reducing to put A in reduced echelon form.
c) Identify the basic columns of A, the free columns of A and the rank of A.
Answer:
After row reducing in any one of a variety of ways, you get the reduced echelon form of A:

Thus there are pivots in columns 1 and 3, so those are the basic columns. The
free columns are 2
and 4, and rank(A) = 2.
2. Consider the inhomogeneous linear system
3x + 2y + z = 13
−x + 4y + 2z = −2
2x + 6y + 3z = 11
a) Write the augmented matrix for the system.
b) Row reduce to echelon form.
c) Find a particular solution to the inhomogeneous system.
d) Determine and describe parametrically all solutions to the corresponding
homogeneous system.
e) Describe all solutions to the original inhomogeneous system.
Answer:
The augmented matrix for the system is
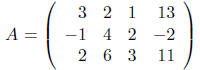
You can row reduce to echelon form, or go all the way to reduced echelon form, which is
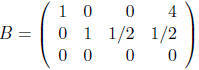
So z is a free variable , and you can find a particular solution by taking z = anything, say z=0.
Then the second line says
y + 1/2z = 1/2, so for z = 0, y = 1/2
The the first line says
x = 4
so our particular solution is (x,y,z) = (4, 1/2, 0)
For the homogeneous system ignore column 4, consider the constants to be 0. Then the reduced matrix says:
y + 1/2 z = 0 , which implies y = -1/2 z, and x = 0
So the general homogeneous solution set is {(0,-1/2 z, z)}.
Scaling by a factor of 2, writing z = 2t, we can say that the general
homogeneous solution is parametrically
described by (x, y, z) = t (0, -1, 2)
So the general solution to the inhomogeneous system is
{(x, y, z) = (4, 1/2, 0 ) + t (0, -1, 2)}
3. Consider the linear system
x + (a + 2)y = a + 2
(a + 1)x + 2y = 3a + 11
For which values of the parameter a does the system have
a) a unique solution
b) no solutions
c) infinitely many solutions
Answer:
The associated augmented matrix is
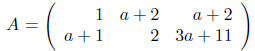
Row reducing to echelon form (without dividing by something that might be zero) we get
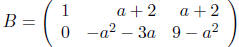
Case 1: If a ≠ 0 or -3, then −a^2 − 3a
≠ 0, so there is a pivot in the second row. Thus the rank
of
the coefficient matrix is 2, and there is a unique solution.
Case 2: If a = -3, then the second line is identically zero, and then
y is a free variable. Thus there
are infinitely many solutions.
Case 3: If a = 0, then the second row is (0 0 9), so there is a pivot
in the augmentation column. The
equations are inconsistent , so no solutions.
4. Let
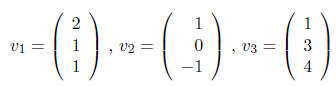
Write the vector
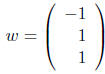
as a linear combination of v 1, v2, v3.
Answer:
Set this up as a system of equations x1v1 + x2v2 + x3v3 = w. The augmented matrix is
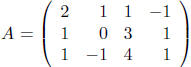
The reduced echelon form of A is

Thus there is a unique solution
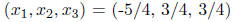
5. List seven 3 × 3 matrices, all with rank ≥ 2, that are
not row equivalent . All matrices listed must
be in reduced echelon form.
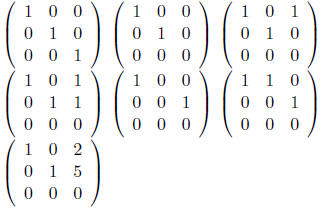
6. Consider the vectors the diagonal of a cube given by
the vector v = (1, 1, 1) and the diagonal of one
of its faces given by w = (1, 1, 0). Determine the lengths of v and w, and the
angle between them.
The vectors are given, so just calculate :
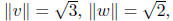
so the angle between v and w is given by
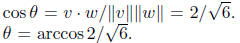
7. Give examples of
(a) A system of four linear equations with 3 unknowns that
has more than one solution .
(b) A system of three equations with 4 unknowns that has no solution .
There is a lot of free play here. Some really simple examples are possible, for example
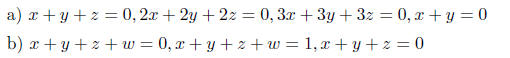
8. Find all vectors in R^4 that are perpendicular (orthogonal) to
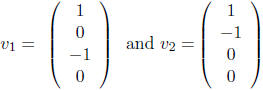
Let w = (a,b,c,d), then we have two equations in 4 unknowns:
w · v1 = 0,w · v2 = 0
This translates to
a - c = 0
a - b = 0
So a = b and a = c, where c and d are free variables. Thus
the complete solutions set is
{(a, b, c, d) = (c, c, c, d)}
Parametrically, that is {c ( 1, 1, 1, 0) + d (0, 0, 0, 1)}
| Prev | Next |