LINEAR ALGEBRA NOTES
8. Vector spaces
vector space: set V of vectors with verctor addition and scalar
multiplication satisfying
for all 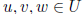 and
and
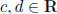
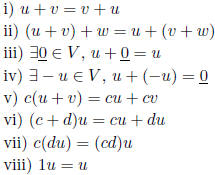
examples: 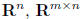 ,P
polynomials,
,P
polynomials, 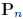 polynomials with degree less
than n, sequences,
polynomials with degree less
than n, sequences,
sequences converging to 0, functions on R, C(R) continuous
functions on R, solutions of
homogeneous systems
subspace of V : subset W of V that is a vector space with same operations
proper subspace of V : subspace but not 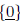 and not V
and not V
examples:
W =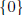 and W = V , subspaces of V
and W = V , subspaces of V
W = lines through origin, subspace of 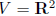
W =planes through origin, subspace of 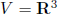
W =diagonal n × n matrices, subspace of 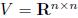
W = 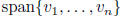 , subspace of V where
, subspace of V where
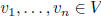
W =convergent sequences, subspace of V =sequences
W =continuous functions on R, subspace of V =functions on R
fact: subset W of V is a subspace of V iff
nonempty: 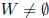
closed under addition: 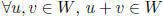
closed under scalar multiplication : 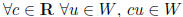
9. Linear independence
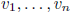 linearly independent:
linearly independent:
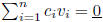 implies
implies 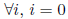
linearly dependent: not independent
parallel vectors: one is scalar multiple of the other
notation 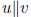
properties :
u, v linearly independent 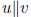
vectors are dependent i one of them is linear combination of the others
subset of lineraly independent set is linearly independent
columns of matrix A are independent i AX = 0 has only trivial solution
columns of square matrix A are independent i A invertible iff detA ≠ 0
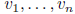 independent,
independent,
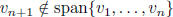 implies
implies 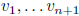 independent
independent
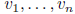 independent,
independent,
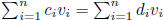 implies
implies 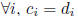
rows of row echelon matrix are independent
leading columns of echelon matrix are independent
10. Bases
S spans W: spanS = W
S is a spanning set of W
basis of V : linearly independent spanning set of V
maximal independent set in V
minimal spanning set of V
standard bases 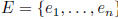 for V :
for V :
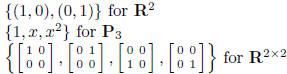
properties:
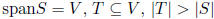 implies T dependent
implies T dependent
all bases of V has same number of vectors
dimension of V : dimV =number of vectors in a basis of V
examples:
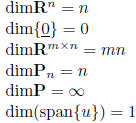
properties:
W proper subspace of V implies dimW < dimV
independent subset of V can be extended to a basis of V
spanning set of V contains a basis of V
11. row, column and null spaces
notation: sizeA = m× n
row space of A: RowA =subspace of 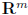 spanned by rows of A
spanned by rows of A
row rank of A: dim RowA
column space of A: ColA =subspace of 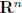 spanned by columns of A
spanned by columns of A
column rank of A: dim ColA
algorithm for basis of RowA:
(i) reduce A to echelon form B
(ii) take nonzero row vectors of B
algorithm for basis of ColA:
(i) reduce A to echelon form B
(ii) take columns of A corresponding to leading columns of B
fact: row rank A equals column rank A
rank A: this common value
null space of A: NullA = 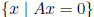 = solution
set of homogeneous system, subspace of
= solution
set of homogeneous system, subspace of 
properties:
A, B row equivalent implies RowA = RowB
A, B row equivalent implies colums of A and columns of B have the same
dependence relations
Ax = b consistent iff b ∈ ColA
rankA + dim NullA = n
12. Coordinates
notation: 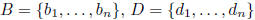 bases for
bases for
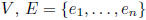 eng standard basis for V
eng standard basis for V
fact: each v ∈ V can be written uniquily as
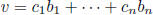
coordinates of v in basis B: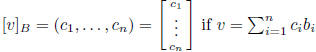
huge fact: 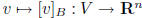 is an isomorphism (
is an isomorphism (![]() are the 'only' finite dimensional vector spaces)
are the 'only' finite dimensional vector spaces)
transition matrix from basis B to basis D: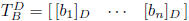 square matrix
square matrix
properties:
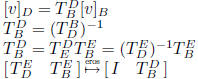
algorithm for finding a basis for
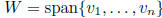 in V :
in V :
(i) find a bases B for V (use standard if possible)
(ii) put the coordinates of the vi's as rows (columns) for a matrix A
(iii) find a basis for the rowspace (columnspace) of A
(iv) use this basis as coordinates to build the basis of W
13. Linear transformations
notation: 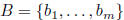 basis for
basis for
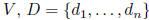 basis for W, E standard basis for V
basis for W, E standard basis for V
linear transformation: L : V → W such that for all
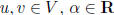
L(u + v) = L(u) + L(v) additive
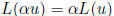 multiplicative
multiplicative
kernel: 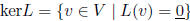
range: 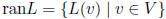
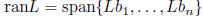
L is one-to-one (1-1): L(u) = L(v) implies u = v
L is onto W: ranL = W
properties:
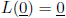
kerL subspace of V
ranL subspace of W
L is 1-1 i 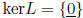
matrix of L: 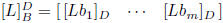
properties:
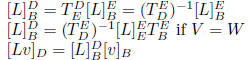
R, S are similar matrices: S = P-1RP for some P
fact: R, S are similar iff 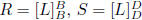 for some L : V → V and bases B, D for V
for some L : V → V and bases B, D for V
(P is the transition matrix)
rank of L: rankL = dim ranL
properties: 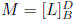
[ranL]D = ColM
[kerL]B = NullM
rankL = rankM
dim kerL = dim nullM
rankL + dim kerL = dimV
14. Eigenvalues and eigenvectors
notation: L : V → V linear transformation,
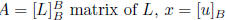 coordinates of u
coordinates of u
eigenvalue problem:
transformation version 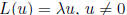
eigenvalue: λ
eigenvector of L associated to λ: u
eigenspace associated to λ: 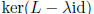
matrix version 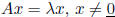
eigenvalue: λ
eigenvector of A associated to λ: x
eigenspace associated to λ : 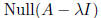
characteristic polynomial: 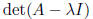
if A~ B then charpoly(A) = charpoly(B)
characteristic equation : λ eigenvalue of A iff 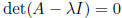
15. Diagonalization
A diagonalizable: A similar to diagonal matrix
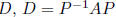
fact: 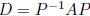 implies
implies

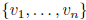 is a basis of eigenvectors with associated
eigenvalues in the diagonal od D
is a basis of eigenvectors with associated
eigenvalues in the diagonal od D
properties:
if 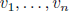 eigenvectors associated to distinct
eigenvalues then they are independent
eigenvectors associated to distinct
eigenvalues then they are independent
if sizeA = n × n and A has n distinct eigenvalues then A diagonalizable
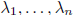 distinct eigenvalues,
distinct eigenvalues,
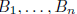 bases for eigenspaces implies
bases for eigenspaces implies
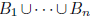 is independent
is independent
algorithm for diagonalization:
(i) solve charachteristic equation to find eigenvalues
(ii) for each eigenvalue nd basis of associated eigenspace
(iii) if the union of the bases is not a basis for the vectorspace than not
diagonalizable
(iv) build P from the eigenvectors as columns
(v) build D from the corresponding eigenvalues
16. Bilinear functional
product of U and V : 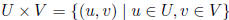
bilinear functional on V : 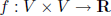 such that
for all
such that
for all
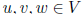 and
and 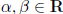
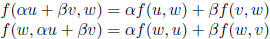
fact: Every bilinear functional f on
![]() is
is
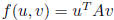 for some
for some 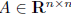
where 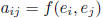
The bilinear functional f can be
symmetric: f(u, v) = f(v, u) for all 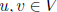
positive semi definite: f(v, v) ≥0 for all v ∈ V
positive definite: f(v, v) > 0 for all 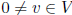
negative semi definite: f(v, v) ≤0 for all v∈ V
negative definite: f(v, v) < 0 for all 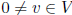
indefinite: neither positive nor negative semidefinite
17. Inner product
inner product: symmetric, positive definite, bilinear functional
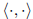
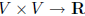
examples of inner products:
dot product (standard inner product) on
![]() :
: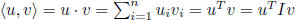
standard inner product on C[0, 1]: (continuous functions on [0,1]),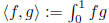
fact: every inner product on
![]() is
is
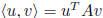 where A is a symmetric (therefore
diagonalizable)
where A is a symmetric (therefore
diagonalizable)
matrix with positive eigenvalues and 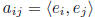
length (norm): 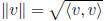
unit vector: 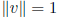
unit vector in the direction of v: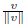
distance: 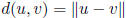
angle: 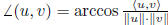
orthogonal: 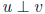 iff
iff
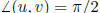 iff
iff 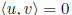
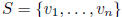 orthogonal:
orthogonal:
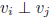 for all i, j
for all i, j
fact: nonzero orthogonal vectors are independent
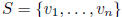 orthonormal: S is orthogonal and
orthonormal: S is orthogonal and
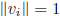 for all i
for all i
Cauchy- Schwartz inequality : 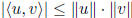
Triangle inequality:
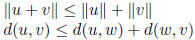
Pythagorean theorem: ![]() implies
implies 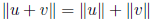
orthogonal complement: 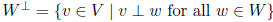 , W is subspace
of V
, W is subspace
of V
properties: W is subspace of ![]()
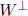 is a subspace
is a subspace
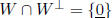
W = span(S), 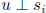 for all i implies
for all i implies
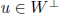
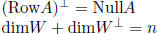
(basis of W) [ (basis of
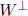 ) is basis of
) is basis of
![]()
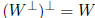
18. Orthogonal bases and Gram-Schmidt algorithm
fact: 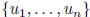 orthogonal basis for a
subspace W of V , y ∈ V
orthogonal basis for a
subspace W of V , y ∈ V
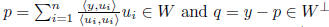
if 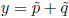 such that
such that
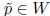 and
and 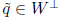 then
then 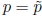 and
and 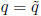
orthogonal projection: 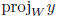 = the unique
p ∈ W such that
= the unique
p ∈ W such that 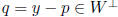
Gram-Schmidt algorithm: for finding an orthogonal basis
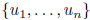 for
for 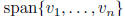
(i) make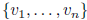 independent if necessary
independent if necessary
(ii) let 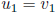
(ii) inductively let 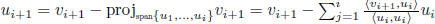
fact: 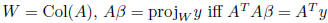
19. Least square solution and linear regression
fact: if W subspace of V , w ∈ W, y ∈ V then
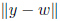 is minimum when
is minimum when
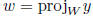
fact: 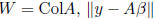 is minimum
is minimum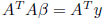
least square regression line ax + b: data 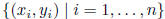
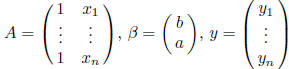 , β makes
, β makes
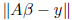 minimum, that is,
minimum, that is,
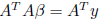
| Prev | Next |