Linear & Absolute Value Equations
Overview
• Section 1.1 in the textbook:
– Solving Linear Equations
– Contradictions and Identities
– Absolute Value Equations
Solving Linear Equations
Definition of a Linear Equation
• Linear Equation: where all the variables
are raised to the first power
• Linear Equation (in one variable): has
the form ax + b = 0 where a and b are
constants and a ≠ 0
Solving Linear Equations in One Variable
• To solve more complex equations :
– Apply the distributive property
– Combine like terms
– Isolate the variable on one side of the equation
– Apply the Addition Property of Equality
– Apply the Multiplication Property of Equality
– Don’t forget to simplify
– Check
Solving Linear Equations in One
Variable (Example)
Ex 1: Solve: 3(x – 5) – (x + 2) = 4
Ex 2: Solve: -2(7 – 3x) + 2x = 2 – (1 – x)
Solving Linear Equations with
Fractions
• While it is certainly possible to work with
fractions in an equation , it is often easier to
eliminate them
• How do we add two UNLIKE fractions?
– Look for an LCD
• We can use the LCD to help us eliminate the
fractions in an equation
• What kind of mathematical statement is adding
½ + ¼?
– Expression
• The rules are a bit different with an
equation
• What must always be remembered when
performing operations on equations?
– “What you do to one side, you must do to the
other”
• How can we use the LCD to help us solve
an equation with fractions?
Solving Linear Equations with
Fractions (Example)
Ex 3: Solve:
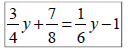
Ex 4: Solve
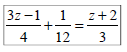
Contradictions & Identities
Identities and No Solutions
• Can only happen when the variable drops
out on BOTH sides of the equation
• Determine whether the resulting statement
is true or not:
– If yes, then the equation has an infinite
number of solutions and we say the solution is
all real numbers
• Also called an identity
– If no, then the equation has no solution
• Also called a contradiction
Identities and No Solutions
(Example)
Ex 5: Solve: 2(5x – 2) – 2 = 20x – 1 – 5(2x + 1)
Ex 6: Solve:
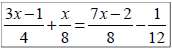
Absolute Value Equations
• Absolute Value: Distance from 0 as
viewed on a number line
– Thus can only be positive or 0
• If |x| = a (a > 0), then x = a or x = -a
-> {a, -a} (written in set notation)
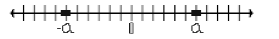
• If |x| = 0, then x = 0 -> {0}
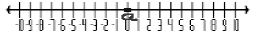
• If |x| = a (a < 0), what is the solution? Ø
• Before applying the definition of absolute
value, the absolute value must be
ISOLATED first
– VERY important!
– The absolute value must be ISOLATED
before the definition of absolute value can be
applied!
Absolute Value Equations
(Example)
Ex 7: Solve:
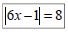
Ex 8: Solve:
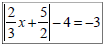
Ex 9: Solve:
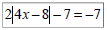
Ex 10: Solve:
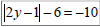
Summary
• After studying these slides, you should
know how to do the following:
– Solve Linear Equations in One Variable
including Identities and Contradictions
– Solve Absolute Value Equations
• Additional Practice
– See the list of suggested problems for 1.1
• Next lesson
– Formulas and Applications (Section 1.2)
| Prev | Next |