Linear Equations and Regular Matrices
In this handout we will introduce some basic facts from
linear algebra .
A system of m linear equation in n variables is often written in the form
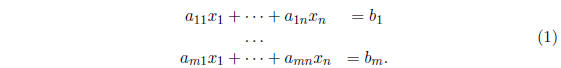
In general, a system like (1) may have no solutions (in
which case we
say that the system is inconsistent or overdetermined), infinitely many solu-
tions (in which case we say that the system is underdetermined), or exactly
one solution. If 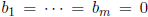 , then we say that the
system (1) is
, then we say that the
system (1) is
homogeneous.
Exercise 1 Show that 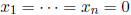 is always a
solution of a homoge -
is always a
solution of a homoge -
neous system and conclude that a homogeneous systems has infinitely many
solutions if and only if it has a non- zero solution .
The coefficient matrix of (1) is the matrix
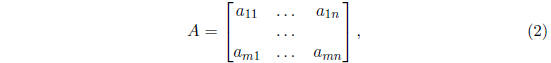
and the extended or augmented matrix of (1) is the matrix
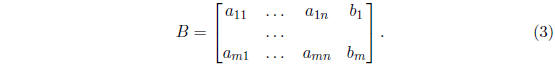
Exercise 2 Find the coefficient matrix and the
augmented matrix for the
following system of linear equations :
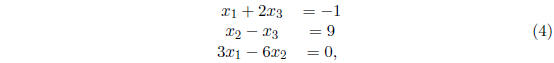
and find the homogeneous system with the same coefficient
matrix, as well
as its augmented matrix.
The columns of B can be written as n + 1 column vectors
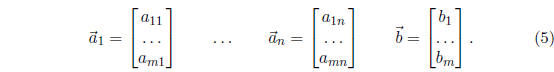
A linear combination of vectors
 is a vector
is a vector
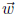 that can be
that can be
expressed as
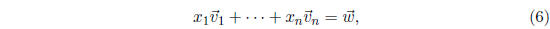
where 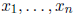 are scalars,
that is, numbers.
are scalars,
that is, numbers.
In the notation of (5), the system (1) can be written as
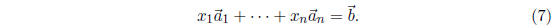
To see this, note that
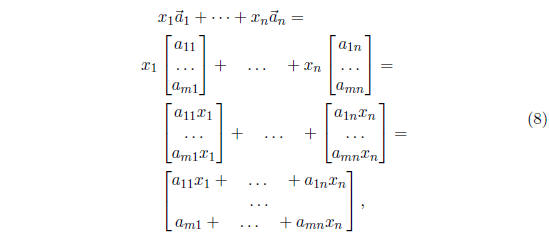
and the last line of (8) is equal to
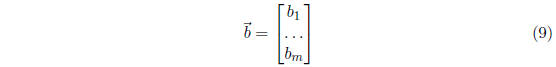
if, and only if, the equations in (1) are satisfied. It
follows that (1) is
consistent (i.e, has a solution) if and only if
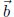 is a linear combination of
is a linear combination of
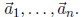
Exercise 3 Let
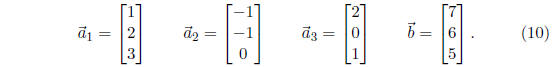
It can be shown that 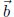 is a linear combination of
is a linear combination of 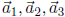 . That is, there
. That is, there
exist numbers 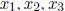 such that
such that
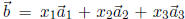 . Write down
. Write down
a system of linear equations whose solution will give you these numbers
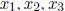 . What is the coefficient matrix A for this
system?
. What is the coefficient matrix A for this
system?
A set of vectors ![]() is
linearly dependent if one of these vectors can
is
linearly dependent if one of these vectors can
be expressed as a linear combination of the other vectors. For example, if
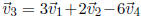 , then the vectors
, then the vectors
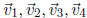 are linearly dependent. An
are linearly dependent. An
equivalent definition that is more commonly used in the literature says that
![]() are linearly
dependent if there exist scalars (numbers)
are linearly
dependent if there exist scalars (numbers)
![]() ,
,
not all of them zero, so that
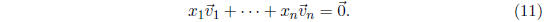
This latter definition gives an interesting connection
with solutions of
homogeneous linear systems. Note that (1) is homogeneous if and only if
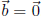 . Thus a homogeneous system (1) has a
non-zero solution if and only
. Thus a homogeneous system (1) has a
non-zero solution if and only
if the columns  of the coefficient matrix A
are linearly dependent.
of the coefficient matrix A
are linearly dependent.
Exercise 4 Consider the vectors
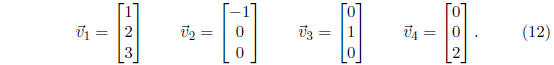
Show that these vectors are linearly dependent in two
different ways:
(a) Pick one of these vectors and express it as a linear combination of the
remaining three vectors.
(b) Find numbers 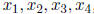 , not all of them zero, such
that
, not all of them zero, such
that
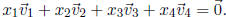
Vectors that are not linearly dependent are called linearly independent.
By rephrasing the second definition of linear dependence we can see that
vectors ![]() are linearly
independent if and only if the equality
are linearly
independent if and only if the equality
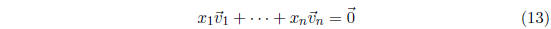
implies that 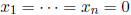 . The
connection between linear de-
. The
connection between linear de-
pendence and solutions of homogeneous systems of linear equations that
we mentioned above can now be rephrased as follows: A homogeneous sys-
tem (1) has no non-zero solution if and only if the columns
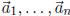 of the
of the
coefficient matrix A are linearly independent. The double negative in the
last sentence becomes easier to understand if we think about it this way: In
Exercise 1 you showed that the zero vector is always a solution of a homo-
geneous system (1). It is the unique solution of this system if and only if
the column vectors of its coefficient matrix A are linearly independent.
Thus if we want to find out whether a (homogeneous) system of linear
equations (1) has a unique solution, we will need to find out whether the
column vectors of its coefficient matrix are linearly independent. It is usually
quite difficult to do this directly from the definition (as you may have found
out while doing Exercise 4). Fortunately, if A is a square matrix , that
is, if A has dimension n × n for some n, there is a shortcut: For every
square matrix A, one can compute a number det (A) called the determinant
of A, and this number tells us whether the column vectors of A are linearly
independent. More precisely , the following holds:
| Prev | Next |