Linear Equations Worksheet-Solutions
9. **Find a pair of points that together with the points (−2, 1) and (2,−2) are
the vertices
of a square.
Answer Case 1: The segment
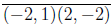 is a side of a square.
is a side of a square.
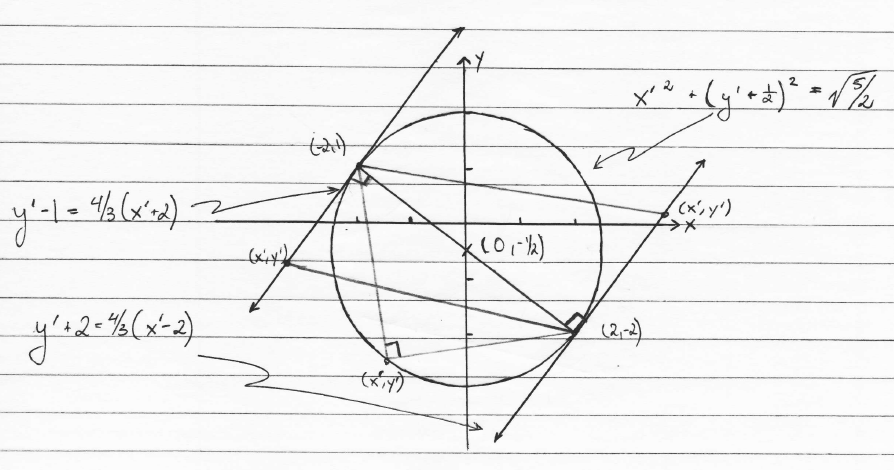
The line through the points (−2, 1) and (2,−2) has the equation
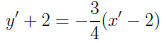
and the distance between these points is
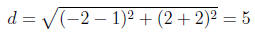
Each of the two points we are looking for needs to lie on a line parallel to the
one
above and also on a line perpendicular to it and passing thru either (−2, 1) or
(2,−2).
That is, we need to solve the systems
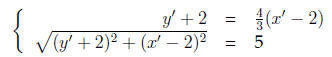
and
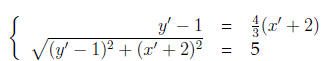
In the first system we substitute for (y' + 2) in the second equation.
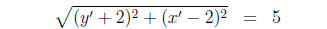 (1)
(1)
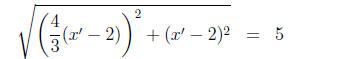 (2)
(2)
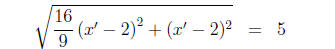 (3)
(3)
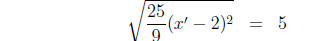 (4)
(4)
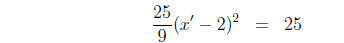 (5)
(5)
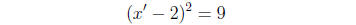 (6)
(6)
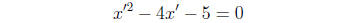 (7)
(7)
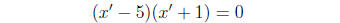 (8)
(8)
Thus we obtain the solutions (5, 2) and (−1,−6). Following the same procedure
for the second system we obtain the solutions (−5,−3) and (1, 5). But our pair
of
solutions must lie on a line parallel to the one thru (−2, 1) and (2,−2), i.e. a
line
with slope m = −3/4 . So the possible solutions are the pairs of points (1, 5), (5, 2) and
(−5,−3), (−1,−6).
Case 2: The segment 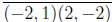 lies on the diagonal of a square.
lies on the diagonal of a square.
In this case we will obtain a smaller square of side length
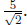 We need to find the
We need to find the
other diagonal, i.e. the line perpendicular to the segment
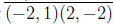 and
passing
and
passing
through its midpoint 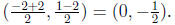 This line has the equation
This line has the equation
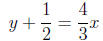
and since half the diagonal is 5/2 , the two points we are looking for need to be
distance 5/2 away from the center of the square (0,−1/2 ) as well as the endpoints of
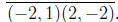 We need to solve the system
We need to solve the system
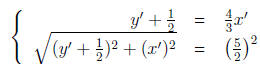
Omitting the algebra we obtain the points
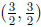 and
and 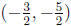 and this is a third
and this is a third
possible solution.
10. ***Find all points such that together with the points (−2, 1) and (2,−2)
they are the
vertices of a right triangle.
Answer We have two cases to consider. First, suppose that the line segment
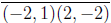 is the leg of a right triangle. Then the third vertex lies on a
line perpendicular
is the leg of a right triangle. Then the third vertex lies on a
line perpendicular
to the line thru (−2, 1) and (2,−2) and passing thru either (−2, 1) or (2,−2).
If (x', y') is the third vertex, then either
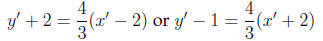
The second and more interesting case is that the line segment
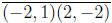 is
the
is
the
hypotenuse of a right triangle. From elementary geometry we recall the Theorem
of Thales which states that the triangle formed by the diameter of a circle and
line
segments joining an arbitrary point on the circle with the endpoints of the
diameter
is a right triangle. Thus we need to find the equation of a circle whose
diameter is
the line segment 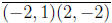 .
.
Using the distance formula we have the diameter
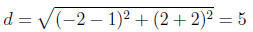
and the midpoint of our circle
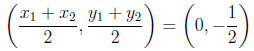
This is the circle of radius 5/2 centered at the point (0,−1/2 ).
The answer is disappointing, because we do not explicitly give the coordinates
of
a point or points. In fact there are infinitely many possibilities, so listing
them
amounts to writing a formula which computes them for us. We have a formula
for the coordinates of every point which solves the problem. If (x', y') is the
third
vertex of the right triangle with vertices (−2, 1) and (2,−2), then either

or
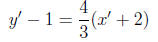
or
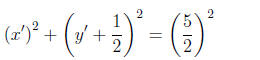


| Prev | Next |