Logarithmic Functions
Definition:
Let a > 0, a ≠ 1. Then logax is the number to which you raise a to get x.
Logarithms are in essence exponents. Their domains are powers of the base and
their ranges are the exponents needed to produce those particular powers.
Example: Demonstrate that log1016 = 2 .
Here the base is 4 and x = 16. To what number do you have to raise 4
in order to get 16? Answer: 2, so
log1016 = 2 .
Example: Show that log1010,000 = 4 .
Here the base is 10, and x = 10,000. What number do you have to raise
10 to, in order to get 10,000 (4 zeros )? Answer: 4, so
log1010,000 = 4.
Example: log10.001 = ?
Here the base is 10, and x = .001 . Write .001 as a power of 10. Since
.001 = 10-3 ,log10.001 = -3
The function
log10 x is known as the common logarithm. Sometimes
you will see the expression log x .
Theorem:
Let a > 0, a ≠ 1 . Then loga x and ax are inverse to each other.
Remark:
This theorem is too difficult to prove here. However, if you let f (x) = ax and
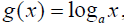 you can show the following.
you can show the following.
a)
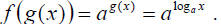 What does this mean? It is a, raised to the
What does this mean? It is a, raised to the
number to which you raise a to get x. So it equals x, that is
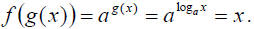
b)
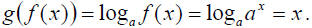
So we haven’t completely proved this theorem, but you can see that
loga x and
ax undo each other.
| Domain of f | f (x) = ax | Range of f |
 |
||
| Range of g |
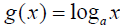 |
Domain of g |
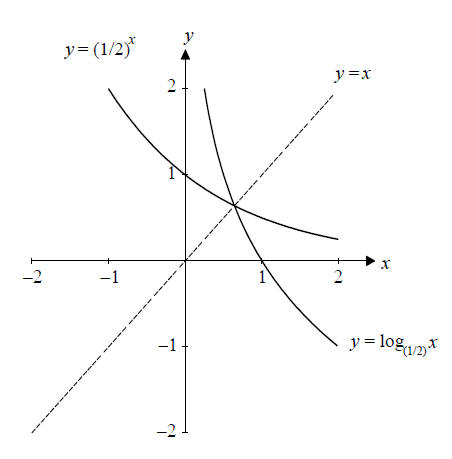
Graphs of Logarithmic Functions:
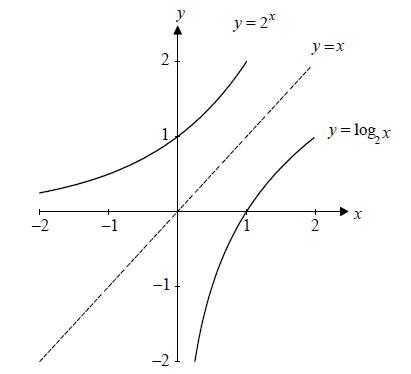
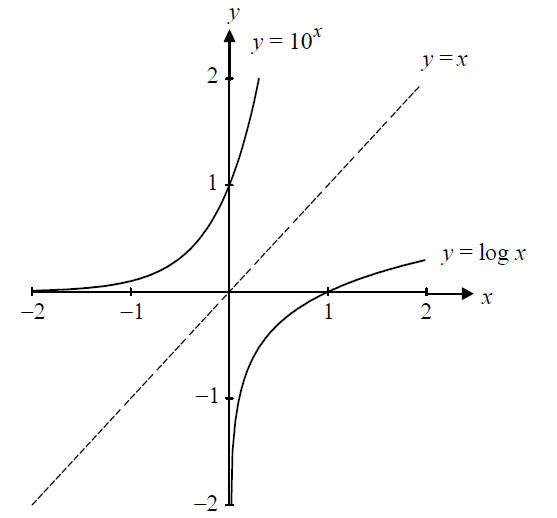
Knowing that
loga xand ax are inverses allows you immediately to graph
loga x If you wish to graph the function
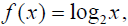 you need only
graph the
you need only
graph the
function g(x) = 2x , and flip it around the line y = x
Solving Exponential Equations
We are now able to solve exponential equations by “getting at” the
exponent of a term .
Example: Solve for x: 2x = 3
Since one can’t write 3 as a power of 2, this rather simple problem can’t be
solved without logarithms. But now, knowing that
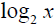 is the inverse of 2x
is the inverse of 2x
one simply “Logs both sides.”
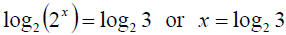
You see that logarithms isolate the exponent.
Example: Solve of x:
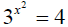
First log both sides:
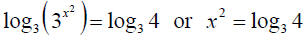
And now take the square root of both sides so that
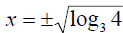
| Prev | Next |