Exponential Functions
Learning Objectives:
1. Evaluate exponential expressions .
2. Graph exponential functions.
3. Define the number e .
4. Solve exponential equations.
1. Evaluate Exponential Functions
Example: f(x) = 3x
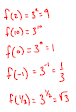
2. Graphing Exponential Functions
An exponential function is a function of the form
f(x) = ax
where a is a positive number and a ≠ 1.
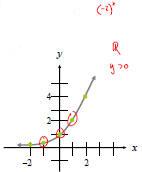
Example:
Graph f(x) = 2x.
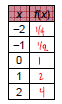
2. Properties of Exponential Functions
Properties of the Graph of an Exponential
Function f(x) = ax, a > 1
1. The domain is the set of all real numbers . The
range is the set of all positive real numbers .
2. There are no x-intercepts; the y- intercept is 1.
3. The graph of f contains the points
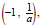
(0,1), and (1, a).
2. Graphing Exponential Functions
Example:
Graph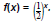 
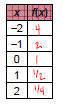
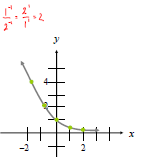
2. Properties of Exponential Functions
Properties of the Graph of an Exponential
Function f(x) = ax, 0 < a < 1
1. The domain is the set of all real numbers. The
range is the set of all positive real numbers.
2. There are no x-intercepts; the y- intercept is 1.
3. The graph of f contains the points
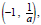
(0,1), and (1, a).
3. The Number e
The number e is defined as the number that the
expression
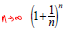
approaches as n becomes unbounded in the positive
direction (that is, as n gets bigger).
e ≈ 2.718
4. Solving Exponential Equations-Basic
Equations that involve terms of the form ax, a > 0, a ≠ 1
are called exponential equations.
Property for Solving Exponential Equations
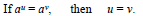
4. Solving Exponential Equations
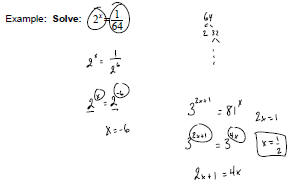
4. Exponential Models
Example:
Newton’s Law of Cooling states that the temperature of a heated
object decreases exponentially over time toward the temperature of
the surrounding medium. Suppose that a pizza is removed from a
400° oven and placed in a room whose temperature is 70°. The
temperature u (in °F) of the pizza at time t (in minutes) can be
modeled by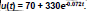 
What will be the temperature of the
pizza after 10 minutes?
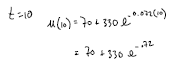
| Prev | Next |