Linear Equations and Graphing
The slope of a linear equation : the price-demand
equation
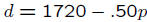
If price increases by $1 how much does demand decrease?
Does this depend on the starting price?
If price increases by $1000 how much does demand decrease?
Does this depend on the starting price?
Is the decrease in demand always .50 times the increase in price?
Slope of a line :
The slope or steepness of a straight line is the same between
any two points on the line. We can reformulate this property of
a line in algebraic terms as follows:
For any two points (x1, y1), (x2, y2) on the line, the ratio of the
change in y (change in y is y2 − y1) to the change in x (x2 − x1)
is the same no matter which two points on the line are chosen .
This common ratio is the slope of the line.
Definition 3 The slope of a line is defined as
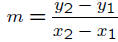
where (x1, y1) and (x2, y2) are ANY two points on the line.
What is the slope of the line defined by the linear
equation
4x − 3y = 12?
What is the slope of the line defined by the linear
equation
d = 1720 − .50p?
Slope of the special cases:
vertical and horizontal lines
Slope formula : 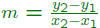 where
(x1, y1) and (x2, y2) are ANY
where
(x1, y1) and (x2, y2) are ANY
two points on the line.
What is the slope of the line defined by the linear
equation
y = −4?
What is the slope of the line defined by the linear
equation
x = 3?
Special forms for linear equations:
Slope- Intercept form .
Definition 4 An equation of the form
y = mx+b
is a linear equation in slope -intercept form.
Put 4x − 3y = 12 into slope- intercept form .
What are m and b?
What do they mean?
Price-demand equation: d = 1720 − .50p.
Put this into slope-intercept form.
What are m and b?
What is the meaning of m? of b?
In general, the graph of an equation y = mx + b defines a
line
with slope m and y-intercept (0, b).
Special forms for linear equations: Point Slope
form.
Definition 5 An equation of the form
y − y1 = m(x − x1)
is a linear equation in point -slope form.
In general, the graph of an equation y − y1 = m(x − x1)
is a line
with slope m passing through the point (x1, y1).
Example: What is the point-slope equation for the line
with a
slope of 3 passing through the point (−4, 6)?
The graph of an equation y −y1 = m(x−x1) is a line with
slope
m passing through the point (x1, y1).
Example: Find an equation for the line passing through the
points (2, 1) and (5, 3).
To use the point-slope form for the line, we need to know
one
point and the slope. In this problem the slope is not given, but
two points are known. To find the slope m, we use the fact that
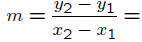
So the point-slope form for the equation using (2, 1) as
the point
is
If we use (5, 3) instead, then the point-slope form of the
equation
is
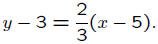
These are two different equations for the same line.
Application: Depreciation.
Linear Depreciation. Office equipment was purchased for $20,000
and is assumed to have a scrap value of $2,000 after 10 years. If
its value is depreciated linearly (for tax purposes) from $20,000
to $2,000:
1. Find the linear equation that relates value (V) in
dollars to
time (t) in years. (Hint: you know two points.)
1. Ans: V = −1800t + 20000. Write a verbal interpretation
of
the slope of the line.
2. What would be the value of the equipment after 6 years?
3. Graph the equation V = −1800t+20000 for 0 ≤ t ≤ 10
Application: Linear Interpolation
The price of a cup of coffee in a coffee bar depends on
the size of
the cup. The 8-ounce cup costs $2.10, but the larger 20-ounce
cup costs $3.30. Without any other information, how could you
estimate the cost of a 10-ounce cup, or a 16-ounce cup?
Sometimes business people use a method known as linear
interpolation.
This means that they assume that the price p of a
cup of coffee and the size q of the cup obey a linear equation.
So the graph of the linear equation is a line and we know two
points on this line: (q, p) = (8, 2.10), (20, 3.30).
Units: The price p of the cup of coffee is given in
dollar.
Size q of the cup of coffee is given in ounces.
two points on the line: (q, p) = (8, 2.10), (20, 3.30).
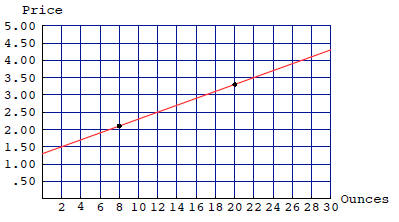
Slope: We know that the price of an 8-ounce cup is $2.10
and
the price of a 20-ounce cup is $3.30. So the change in p is
$3.30−$2.10 = $1.20 and the change in q is 20oz.−8oz. = 12oz..
So the slope is:
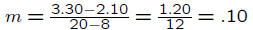
Units for the slope m: dollars per ounce
Slope is $.10 per ounce.
How much does the price increase if the size of the cup
increases
by 4 ounces?
Point-slope form: p − 2.10 = .10(q − 8)
Slope-intercept form: p = .10q +1.30.
y-intercept is $1.30.
Interpretation: The price of a cup of coffee is $1.30 plus
ten
cents an ounce.
Slope-intercept form: p = .10q +1.30.
Use linear interpolation to find the price of a 12-ounce
cup of
coffee:
| Prev | Next |