Rational and Real Numbers
• The Rational Numbers are a field
• Rational Numbers are an integral domain,
since all fields are integral domains
• What other properties do the Rational
Numbers have that characterize them?
Rational Order
Is (Q,+,•) an ordered integral domain?
Recall the definition of ordered.
Ordered Integral Domain: Contains a
subset D+ with the following properties.
1. If a, b ∈ D+, then a + b ∈ D+ (closure)
2. If a , b ∈ D+, then a • b ∈ D+ (closure)
3. For each a ∈ Integral Domain D exactly
one of these holds
a = 0, a ∈ D+, -a ∈ D+ (Trichotomy)
• How can we define the positive set of
rational numbers?
• Verify closure of addition for the positive
set
• Suppose
• Verify closure of multiplication for the
positive set
• Suppose
• Verify the Trichotomy Law
• If a/b is a Rational Number then either a/b
is positive, zero , or negative .
Dense Property
• Between any two rational numbers r and s
there is another rational number.
• Determine a rule for finding a rational
number between r and s. Verify it.
Rational Holes
• Can any physical length be represented by
a rational number?
• Is the number line complete – does it still
have gaps?
Pythagorean Society
• Believed all physical distances could be
represented as ratio of integers – our
rational numbers.
• 500 B.C discovered the following :
• h2 = 12 + 12, h2 = 2, h = ? (not rational)
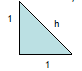
Spiral Archimedes
Rational Incompleteness
• Rational Numbers are sufficient for simple
applications to physical problems
• Theoretically the Rational Numbers are
inadequate
• Are these equations solvable over Q:
4x^2 = 25
x^2 = 13
Rational Incompleteness
• Where does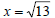 
reside on the
number line?
• Are the Rational Numbers sufficient to
complete the number line?
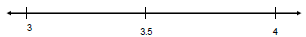
Existence of Irrational Numbers
• Prove 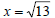is an
irrational number.
Proof:
Eudoxus of Cnidus
Born: 408 BC in Cnidus (on
Resadiye peninsula), Asia Minor
(now Turkey)
Died: 355 BC in Cnidus, Asia
Minor (now Turkey)
• Created the first known definition of the
real numbers .
• A number of authors have discussed
the ideas of real numbers in the work of
Eudoxus and compared his ideas with
those of Dedekind, in particular the
definition involving 'Dedekind cuts' given
in 1872.
Julius Wihelm Richard
Dedekind
Born: 6 Oct
1831 in
Braunschweig,
(now
Germany)
Died: 12 Feb
1916 in
Braunschweig
• His idea was that every real number r
divides the rational numbers into two
subsets, namely those greater than r
and those less than r.
• Dedekind’s brilliant idea was to
represent the real numbers by such
divisions of the rationals.
• Among other things, he provides a
definition independent of the concept of
number for the infiniteness or finiteness
of a set by using the concept of
mapping.
• Presented a logical theory of number and
of complete induction, presented his
principal conception of the essence of
arithmetic , and dealt with the role of the
complete system of real numbers in
geometry in the problem of the continuity
of space.
George Ferdinand Ludwig
Philipp Cantor
Born: 3 March 1845 in
St Petersburg, Russia
Died: 6 Jan 1918 in Halle,
Germany
• Dedekind published his definition of the
real numbers by "Dedekind cuts" also in
1872 and in this paper Dedekind refers
to Cantor's 1872 paper which Cantor
had sent him.
• However his attempts to decide whether
the real numbers were countable
proved harder.
• He had proved that the real numbers
were not countable by December 1873
and published this in a paper in 1874.
What are the Real Numbers?
• Some common definitions
– Extension of the rational numbers to include the
irrational numbers
– Converging sequence of rational numbers, the limit of
which is a real number
– A point on the number line
• Microscope analogy: If you magnify the number
line at a very high power ,
– Would the Real Numbers look the same?
– Would the Rational Numbers look the same or be a
row of dots separated by spaces?
Real Number Properties
• Real Numbers are an ordered field
• Theorem: Every ordered field contains, as
a subset, an isomorphic copy of the
rational numbers
– Thus the Rational Numbers are a subset of
every ordered field
– The Rational Numbers are subset of the Real
Numbers
Upper Bound
• Upper Bound: Let S ⊆ ordered Field F. An
upper bound b ∈ F for S has the property
that x ≤ b for all x ∈ S.
• Least Upper Bound (l.u.b.) is the smallest
possible upper bound.
Example
• Consider the following two sets.
• S = { x | x ∈Q, x < 9 / 2 }
• T = { x | x ∈Q, x^2 < 2 }
• Does an upper bound for S and T exist in
Q?
• Does a l.u.b. for S and T exist in Q?
Dedekind Completeness
Property
• Let R be an ordered field. Any nonempty
set S ⊆ R which has an upper bound must
have a least upper bound.
• Are the Rational Number complete?
• Are the Real Numbers complete?
Extension of Rational Numbers
into Real Numbers
• Theorem: There exists a Dedekind
complete ordered field.
• Verifying requires constructing it.
– Extension using decimal expansion
– Let R be the set of all infinite decimal
expansions and adopt the convention that
0.9999… = 1.0000…
– Can prove completeness holds, but very
difficult
• Theorem: There exists a Dedekind
complete ordered field.
– Extension using Dedekind cuts which are
pairs of nonempty subsets of Q such that for
any c ∈ Q: A = { r | r < c} and B = { r | r > c}
– Think of the cuts as representing the real
numbers
– The set of all cuts is a complete ordered field
Characterization of the Reals
• Any other Dedekind complete ordered field
is an isomorphic copy of the Real
Numbers.
– R is an extension of Q
– R is an ordered field where Q+ ⊂ R+
Density of Real Numbers
• If a, b ∈ R with a < b, there exists a
rational number m/n such that
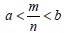
• If a, b ∈ R with a < b, there exists an
irrational number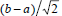 
such that
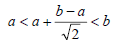
| Prev | Next |