Differential Equations
Solving Systems of First-Order, Linear, Homogeneous Equations with
Constant Coefficients
(Sections 7.5, 7.6, and 7.8)
When: This technique can be used to solve systems of first-order,
linear, homogeneous equations
with constant coefficients . Such a system would look like :
In matrix form, this is:
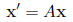
where A is the n*n matrix A = (aij).
What: We want to find the eigenvalues of this matrix A. We will use the
eigenvectors and
eigenvalues to form our general solution. If
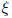is the eigenvector associated to the eigenvalue r, we
will get pieces in our general solution of the form
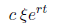
with appropriate alterations made for complex and repeated eigenvalues.
How:
•Check that you have a system of first-order, linear, homogeneous equations
with constant
coefficients.
•Write the system in matrix form:
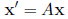
•Find the eigenvalues of A by solving
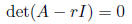
for r.
•There are three cases:
1. Distinct real eigenvalues :
For each real distinct eigenvalue r, you will need to find an associated
eigenvector
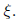You do this by choosing
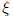to solve the system:
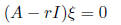
Then, for each such real distinct eigenvalue, you get a piece in your general
solution
of the form:
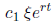
2. Complex eigenvalues:
Eigenvalues are roots of the characteristic polynomial that you get from the
determinant above. We know that complex roots occur in conjugate pairs. Suppose
that our eigenvalues are
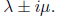Then, find an eigenvector
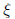associated to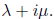
It should satisfy:
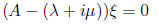
Split
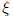into its real and imaginary parts:
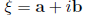
hen, this pair of eigenvalues will contribute two terms to the general solution:
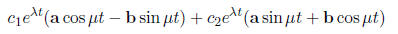
3. Repeated eigenvalue:
Suppose r is a repeated eigenvalue with multiplicity k . If you are able to
find k
linearly independent eigenvectors
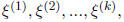then you just get the k pieces:
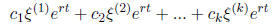
If you cannot find k independent eigenvectors associated to the eigenvalue r,
then you need to find generalized eigenvectors.
For k = 2, this means that you first need to find an eigenvector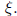
That is
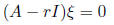
Then, you need to find the generalized eigenvector
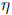satisfying:
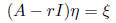
With these, then this eigenvalue will contribute the following two terms to
the
general solution:
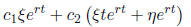
For k = 3, you need to find
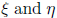as above. In addition , you will need another
generalized eigenvector
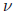satisfying:
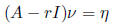
Then, this eigenvalue will contribute the following three terms to the
general solu-
tion:
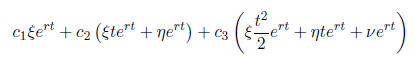
•If given, use an initial conditions to resolve for the unknown constants .
•Check your solution by taking the derivatives and comparing it to the original
equation.
Examples:
1. Find the general solution of the system of equations:
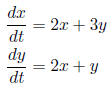
•In matrix form, this is:
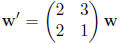
•To find the eigenvalues, we look at:
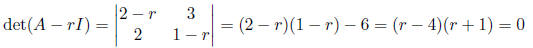
Thus, our eigenvalues are r1 = 4 and r2 = -1.
•The first of these eigenvalues r1 = 4 is a real distinct
eigenvalue. We need to find
an associated eigenvector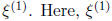 
will satisfy:
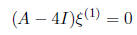
Since
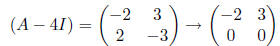
we see that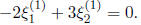 
Thus, we
may use:
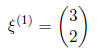
•The second of these eigenvalues r2 = -1 is also a real
distinct eigenvalue. We need
to find an associated eigenvector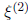 
. Here,
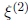will satisfy:
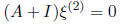
Since
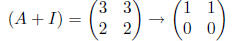
we see that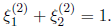 
Thus, we
may use:
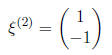
•Thus, our general solution is:
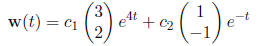
2. Find the general solution of the system of equations:
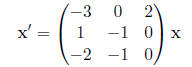
•This first- order homogeneous system of linear
differential equations is already in
matrix form. So, no rewriting is necessary.
•We need to find the eigenvalues. This can be done by examining:
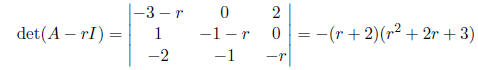
Thus, the eigenvalues are r1 = -2 and
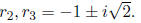
•For the distinct real eigenvalue r1 = -2, we need to find
an associated eigenvector
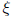. Here 
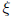satisfies:
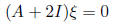
We see that
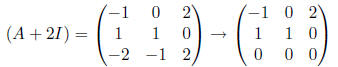
Thus, we know that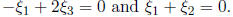 
.
So, we may use:
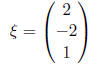
This eigenvalue, then, contributes the following term to the general solution:
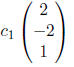
•For the complex pair of roots
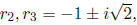we need to find an eigenvector
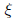
associated to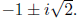 
Here,
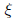satisfies:
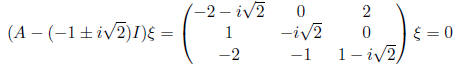
Thus, we see that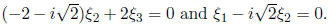 
So,
we may choose
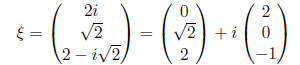
Hence, these eigenvalues will contribute the following two
terms to the general
solution:
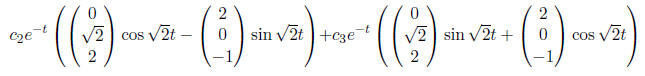
•So, our general solution is:
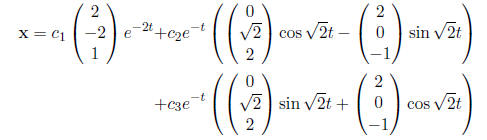
3. Find a general solution to the system of equations:
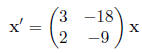
•This first-order homogeneous system of linear equations
with constant coefficients
is already in matrix form, so we don't need to do anything here.
•We need to find the eigenvalues of the matrix. We can do this by examining:
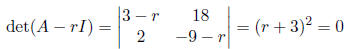
Thus, there is one eigenvalue r = -3 with multiplicity 2.
•To begin, we need to find an eigenvector associated to r = -3. Since
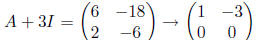
we see that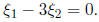 
Thus, we
may choose:
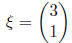
We, also, see that this is the only independent
eigenvector that we can find (only
one row of zeros in the reduced matrix ). So, we need to find a generalized eigen-
vector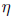 
satisfying:
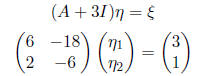
Thus,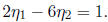 
So, we may use:
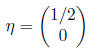
•Then, the general solution to this system of equations is:
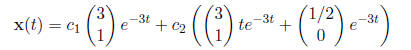
Here is one for you to try with some assistance and a couple for you to try without assistance.
4. Find the general solution to the system of equations:
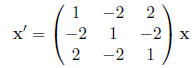
•Check that this is a first-order homogeneous system of
linear equations with con-
stant coefficients.
•Find the eigenvalues of A by looking at det(A - rI) = 0.
•For each real, distinct eigenvalue, find an associated eigenvector.
•For each pair of complex eigenvalues, find an associated
eigenvector and break it
into its real and imaginary parts.
•For each real eigenvalue of multiplicity k find either k
independent eigenvectors or
find an eigenvector and the necessary generalized eigenvectors.
•Form your general solution:
•Take the derivative of the solution and plug in to check your work.
5. Find the general solution for the following system of differential equations :
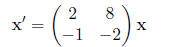
6. Find the general solution for the following system of differential equations:
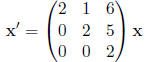
| Prev | Next |