Math 1111 Test 2
Each question is worth 5 points. Attach any scratch paper.
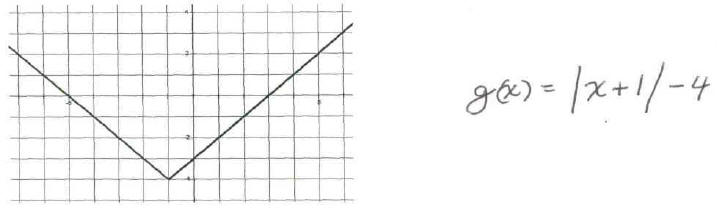
1. The graph of g (x) below is a transformation of the function f(x) = |x|. Find
the function g(x).
2. The graph of g (x) below is a transformation of the function f(x) = x3. Find
the function g(x).
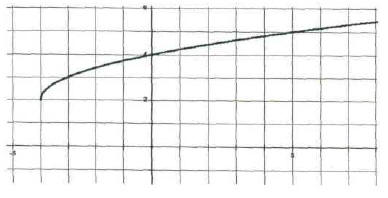
3. Identify the common function and the transformation shown in the graph. Write
an equation for the function
shown in the graph.
Common Function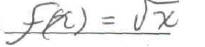 
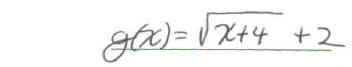
4. Describe the transformation from the common function that occurs in the
function. Then sketch its graph.
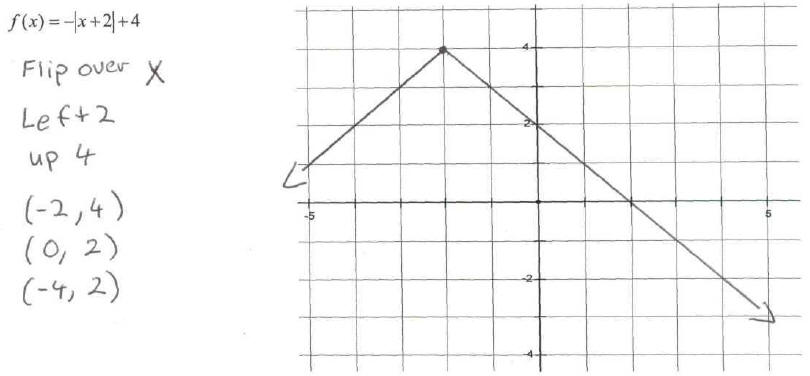
5. Describe the transformation from the common function that occurs in the
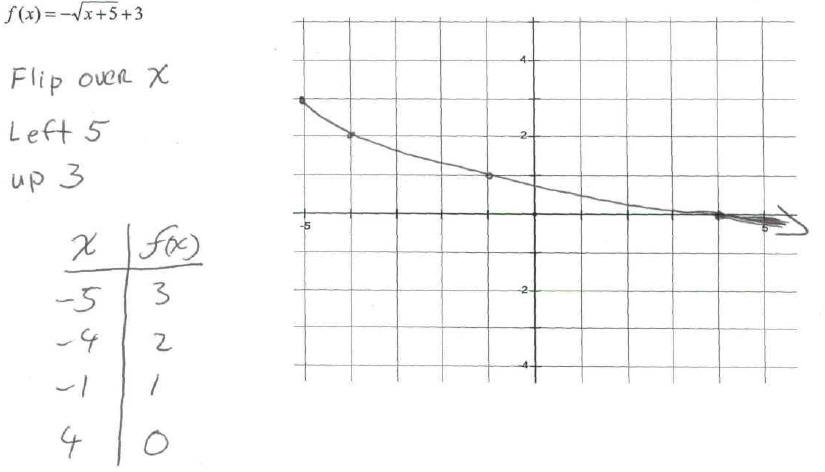
function. Then sketch its graph.
6. Given: f(x) = 2x-3 and g(x) = 3x-5
a) Find
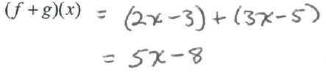
b) Find
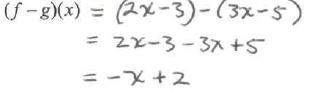
c)
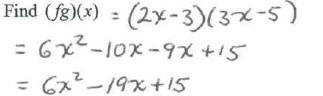
d) Find
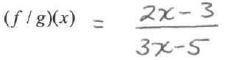
7. Given: f(x) = x2-4 and g(x) = x + 2.
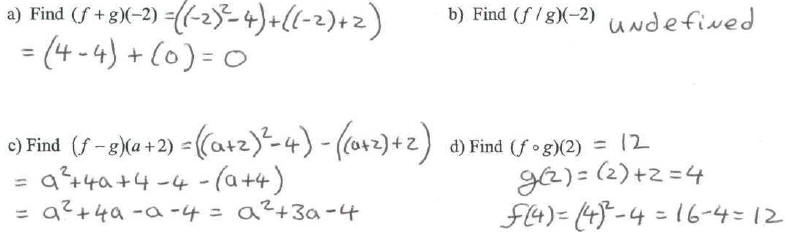
8. Given: f(x) = x2 and g(x) = 2x + 5
9. Find the inverse of f(x) and then verify that f(f-1(x)) = x.
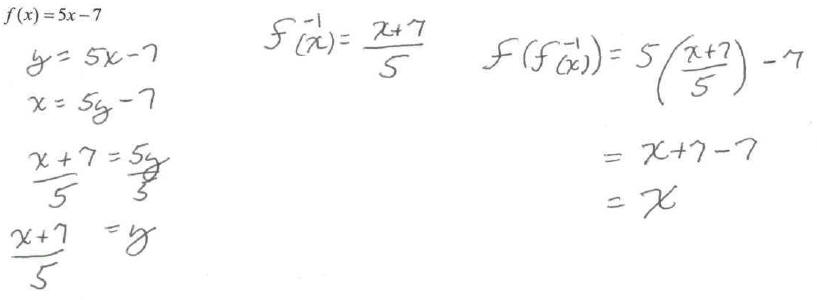
10. Show that f and g are inverses functions. f(x) = 4-3x
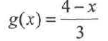
a) Graphically (include identity function) 
b)
Algebraically
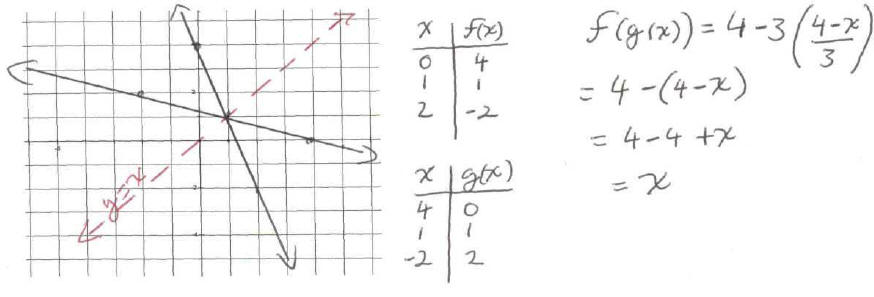
11. Produce the inverse relation. Is the new relation a
function?
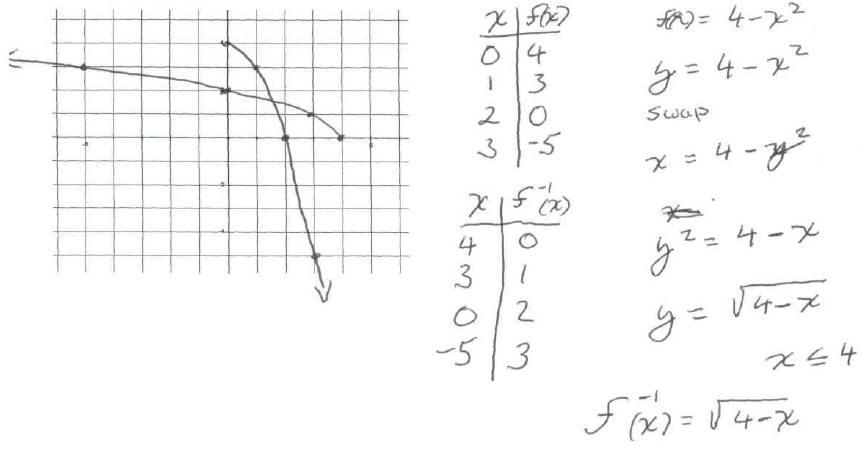
12. Find the inverse function of f Then graph both f(x) and
f-1(x) on the same set of coordinate axis.
f(x) = 4 - x2 for x ≥ 0
13. Does f(x) = (x + 2)2 - 4, x ≥ -2 have an inverse function? If yes, produce
the inverse function.
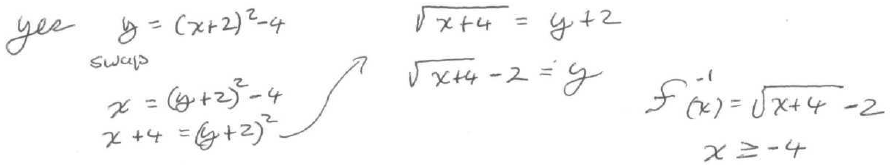
14. Does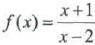
have an
inverse function? If yes, produce the inverse function.
15. Identify the vertex , the y- intercept and the x -intercept(s) of the following
quadratic functions.
f(x) = -3(x-3)2 +12
Vertex (3,12)
^-intercept ( 0,-15)
x-intercepti1 ( 1, 0)
x-intercept2 (5,0)
16. Identify the vertex , the y- intercept and the x -intercept(s)
of the following quadratic functions .
g(x) = 2(x-3)2+S
Vertex ( 3,8)
y-intercept (0,26)
x-intercept1: No x-intercepts
x:-intercept2 ×
17. Identify the vertex , the y- intercept and the x -intercept(s)
of the following quadratic functions .
k(x) = -3x2 + 1 8x - 1 5
Vertex (3,12)
y-intercept (0,15)
x-intercept1 (1,0)
x-intercept2 (5,0)
18. Find the quadratic function that has a vertex of (3,
12) and contains the point (7, -36).
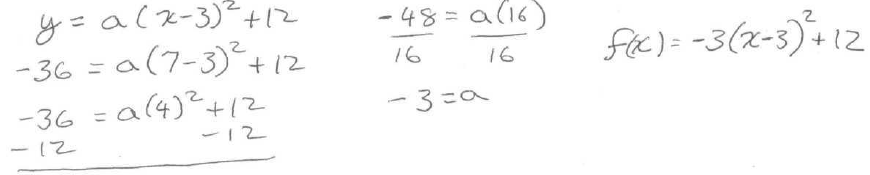
19. Determine the x-intercepts of the graph visually. Then find the x-intercepts
algebraically to confirm
your results.
20. Find two quadratic functions, f(x) that opens upward and g(x) that opens
downward whose graphs have
(-4, 0) and (2, 0) for x-intercepts.
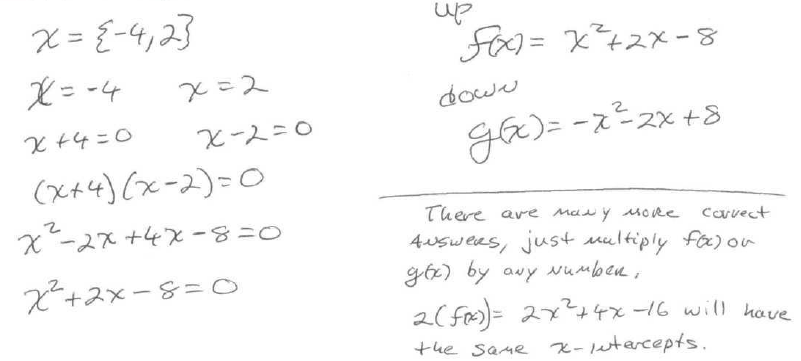
| Prev | Next |