Math 1113 Final Exam
1. (16pts) Determine which elements of the set
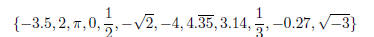
are
a. Real number :
b. Rational number :
c. Irrational number:
d. Integer:
2. (16pts) Let A = (-4,∞), B = (-5, 1), C = (2, 3) and D =
(-∞, 5).
Find A U B , A ∩ B, B U C, B ∩ D.
3. (15pts) Solve the following linear inequalities , denote
the solution sets in
interval notations.
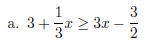
b. 2x - 3 < 7 and 7 - 3x < -2
c. 1 < 1 - 5x < 5
4. (20pts) Solve absolute value inequalities , use interval
notation to denote
the solution sets.
a. 6 - |3 - 2x| < ¡3
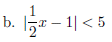
5. (10pts) Let P(-3,-2),Q(5,-4) be two points in the xoy
plane. Find:
(1) The distance between P and Q.
(2) The coordinates of the midpoint between P and Q.
6. (20pts)
(1) Write the equation of the circle with center at (5,-1) and passing
through (1,-3).
(2) Find the center and radius of the circle
x2 + y2 - 4x + 8y + 2 = 0
7. (10 pts) Find the intercepts of the graph of equation x2 + y = 4
8. (15pts)Find the equation of the line
(1) through points (3,-1) and (-2, 5),
(2) through (-1, 4), parallel to x - y = 3,
(3) through (-3,-2) and perpendicular to y = 2x - 10.
9. Let f(x) = 3x2 and g(x) = x + 3. Find the following.
(a) f(3)
(b) g(x + h) - g(x)
10. Fill in the blanks:
The graph of function f(x) = -2|x + 1| - 4 can be obtained by the
following process: Shift the graph of function f(x) = |x| to the (cir-
cle one: right/left/up/down ? ) __(how many ?)units, then (cir-
cle one: stretch/shrink?) by a factor of __(how much?) and then
__(to handle the negative sign ). Finally we need to shift it (circle one:
left/right/up/down?) __(how many?) units.
11. (20pts)Graph the function y = -2|x + 1| by transformation.
12. (10pts) Determine algebraically whether the function
f(x) = 3x3 + |x| is
even, odd or neither.
13. (10 pts) Determine whether function
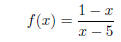
is one-to-one .
14. (10pts) Find the inverse function of
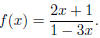
15. (15pts) Let f(x) = x2 + 6, g(x) =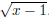 ,
h(x) = 2x.
,
h(x) = 2x.
(a) Find (f ο g)(x).
(b) Evaluate (g ο f)(2).
(c) Find f ο g ο h
16. (16pts) Let f(x) = -2x2 - 12x - 7. Write f(x) into
standard form and
a. Find the vertex of the graph of f(x).
b. Find the range of f(x).
c. Find the minimum or maximum value of f(x).
d. Identify the intervals on which f(x) is increasing or decreasing.
17. (8pts) Solve the following inequalities, use interval
notation to denote the
solution sets.
(1) x2 - x - 42 < 0
(2) x(x - 1)(x + 2) ≥ 0
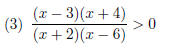
18. (20pts) Simplify the following expressions.
(1) (-3 + 2i) - 3(5 - 3i)
(2) (3 - 4i)(-5 - i)
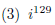
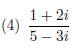
19. (16pts)
(a) Use synthetic division to find the quotient and remainder when 2x3 - 4x -
40 is divided by x + 2.
(b) Use synthetic division to determine whether 3 are zeros of the poly-
nomial
p(x) = x3 - 2x2 - 5x + 6
and then factor p(x) completely.
20. (10pts) Find the roots and their multiplicity for each
equation , state the
degree of the equation.
(a) 2x7 - 72x5 = 0
(b) (x - 2)2(3x - 1)3(x - 3) = 0
21. (10pts)Find a polynomial equation with real
coefficients that has the fol-
lowing given roots
(a) 4, 2i
(b) 1, -i, 2 + i
22. (15pts) Solve the following equations:
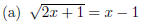
(b) |x + 5| = |3 + 2x|
(c) x4 - 14x2 + 45 = 0
23. (16pts) Convert the angles from degree to radian or
vice versa.
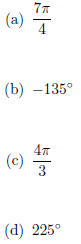
24. (12pts)Find the following function values:

25. (10pts) Assume α is a second quadrant angle and cos α
= -3/5, find sin α
and tan α.
26. (bonus 20 pts)
(a) Use the definitions to prove the fundamental identity:
sin2(α) + cos2(α) = 1
(b) Simplify the following expressions :
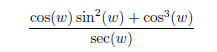
| Prev | Next |