Math 121, Practice for Test 4
The test will cover the following topics and sections from
the text.
• Sections 9.1 and 9.2: systems of linear equations . Key types of problems
included solving
linear systems with 2 or 3 variables . Setting up and solving word problems
involving lin-
ear systems of equations. Recognizing inconsistent, dependent and independent
systems of
equations.
• Sections 10.1, 10.2, and 10.3: Gaussian elimination , the algebra of
matrices, inverses of
matrices. Key types of problems include converting systems of equations to
matrix form
and solving the system using elementary row operations . Matrix addition and
multiplication,
writing linear systems in matrix form. Finding inverses of matrices 2 by 2 or 3
by 3. Recognizing
singular matrices that don't have inverses. Solving systems of linear equations
using the matrix
inverse.
• Sections 11.1 and 11.5: sequences and summation notation , the binomial
theorem . Key
types of problems include, using summation notation, finding terms of sequences ,
binomial
expansions, and finding specific terms in a binomial expansion.
Some practice problems are as follows:
1. Solve each system of equations if possible.
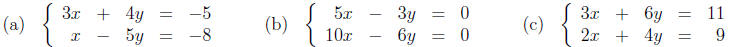
2. A motorboat traveled a distance of 120 miles in 4 hours
while traveling with the current.
Against the current, the same trip took 6 hours. Find the rate of the boat in
calm water and
find the rate of the current.
3. A broker invests $25,000 of a clients' money in two different municipal
bonds. The annual
rate of return on one bond is 6%, and the annual rate of return on the second
bond is 6.5%.
The investor receives a total annual interest payment of $1555 from the two
bonds . Find the
amount invested in each bond.
4. Solve the following systems of equations.
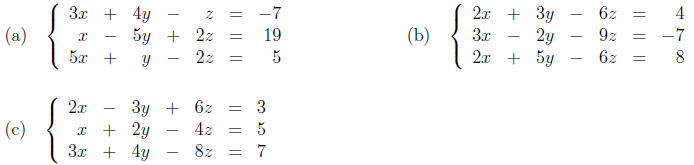
5. The equation of a (nonvertical) plane can be written in
the form z = ax+ by+ c where a, b,
and c are numbers. Find the equation of the plane that contains the points (2,
1, 1), (-1, 2, 12)
and (3, 2, 0).
6. A coin bank contains only nickels, dimes, and quarters.
The value of the coins is $2. There
are twice as many nickels as dimes and one more dime than quarters. Find the
number of each
coin in the bank.
7. Consider the following systems of equations. For each system, find the values
of k for which
there (if possible), (i) one solution, (ii) no solution, (iii) infinitely many
solutions?

8. Write the systems of equations in 1(a) and 4(a) as
augmented matrices, and solve them
using Gaussian elimination.
9. The following are augmented matrices for a systems of equations in the
variables 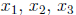
and 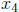 , find the solutions to the systems of
equations.
, find the solutions to the systems of
equations.
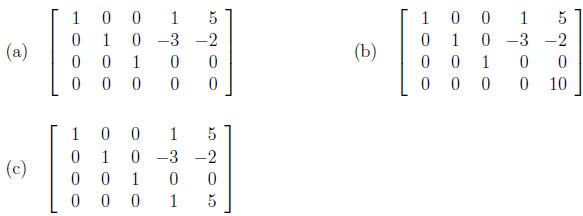
10. Let 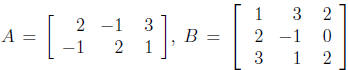 and
and
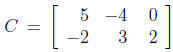 .Find the
.Find the
following, if possible.
(a) AB (b) BA (c) A + B (d) 5A - 3C (e) AC.
11. Determine whether it is possible to find the product AB for matrices of the
given sizes, if
so, determine the size of AB. Same question for BA.
(a) A is a 3 × 3 matrix, B is a 3 ×1 matrix.
(b) A is a 3 × 5 matrix, B is a 3 × 5 matrix.
(c) A is a 5 × 3 matrix, B is a 3 × 5 matrix.
(d) A is a 3 × 2 matrix B is a 2 × 3 matrix.
12. Write the following matrix equation as an equivalent system of equations.
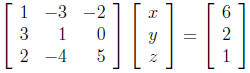
13. Find the inverses of the following matrices (if they exist).
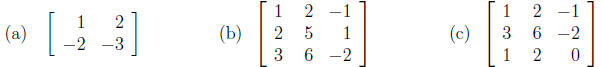
14. Consider the following systems of equations:
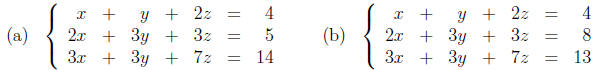
Solve these systems using the fact that the inverse of
 is
is 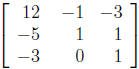 .
.
15. Find the first three terms and the 8th term of the
sequence whose nth term is 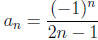 .
.
16. Find the first three terms of the recursively defined sequence
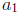 = 5, and
= 5, and 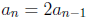 .
.
17. (a) Evaluate the sum 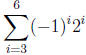 .
.
(b) Write 8 + 10 + 12 + 14 + 16 + 18 in summation notation.
18. Expand the binomial 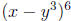 .
.
19. Find the fourth term of (x + 2y)12.
20. Find the term that contains b9 in the expansion of
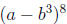 .
.
Further Practice: See Test 4 from Autumn 2004, Winter 2005, Winter 2006,
Autumn 2006.
| Prev | Next |