Dividing Fractions
1. A bread problem: If one loaf of bread requires 1 ¼
cups of flour, then how many loaves
of bread can you make with 10 cups of flour? (Assume that you have enough of all
other
ingredients on hand.)
a.) Solve the bread problem by drawing a diagram. Explain your reasoning.
 |
← one whole cup of flour |
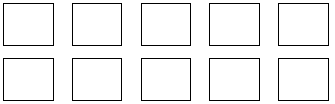 |
← 10 cups of flour |
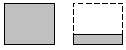 |
← 1 ¼ cups of flour |
| how many times can we fit 1 ¼ cups into 10 cups? (measurement division) |
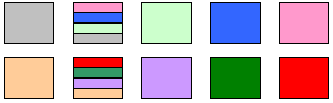
| If each 1 ¼ cup of flour is a different color , we
can easily see that 1 ¼ cups fits into 10 cups exactly 8 times! |
b.) Write a division problem that corresponds to the
bread problem. Solve the division
problem by “inverting and multiplying.” Verify that your solution agrees with
your
solution in part (a).
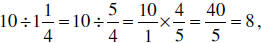 which is the same
solution we found in part (a).
which is the same
solution we found in part (a).
2. A measuring problem: You are making a recipe that
calls for 2/3 cup of water, but you
can’t find your 1/3 cup measure. You can, however, find your ¼ cup measure. How
many
times should you fill your ¼ cup measure in order to measure 2/3 cup of water?
a.) Solve the measuring problem by drawing a diagram . Explain your reasoning.
 |
← one whole cup of water | ||
 |
← 2/3 of a cup of water |
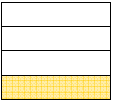 |
← ¼ of a cup of water |
| how many times can we fit the quarter cup into
the 2/3 cup ? (measurement division) |
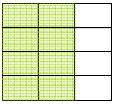 |
← 2/3 of a cup of water but represented as 8/12 |
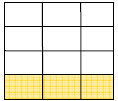 |
← ¼ of a cup of water but represented as 3/12 |
 |
 |
| Now the question is: How many times can I fit a group of 3 rectangles into a group of 8 rectangles? |

If we re-write the problem this way, then we have a
relatively easy division problem involving
whole numbers . How many times does a group of 3 fit into a group of 8 ?
2 times, with 2 things left over, which is 2/3 of the divisor. So the answer is:
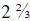 .
.
b.) Write a division problem that corresponds to the
measuring problem. Solve the division
problem by “inverting and multiplying.” Verify that your solution agrees with
your
solution in part (a).
We wanted to solve 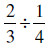 , so
if we invert and multiply we get
, so
if we invert and multiply we get 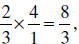 which
agrees with
which
agrees with
our answer above. Is the inverting and multiplying quicker ? Sure, that’s why we
use it. Is it
easy to understand why it works? Well....if you have seen the pictures a few
times it begins to
make sense. That’s why we use the pictures. They both have their place.
3. Write a “how many groups ?” story problem for 4 ÷2/3 ,
and solve your problem in a
simple and concrete way without using the “invert and multiply” procedure.
Explain your
reasoning. Verify that your solution agrees with the solution you obtain by
using the
“invert and multiply” procedure.
Janice has 4 yards of ribbon and she wants to cut it into
strips that are 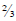 of a yard long. How
of a yard long. How
many strips (or fractions of strips ) can she get?
Let’s try to talk our way through this without using
pictures, perhaps the way a child might who
can add and subtract fractions but may be a little fuzzy on division.
If she cuts one strip, that’s
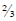 of a yard used up; so she has
of a yard used up; so she has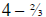 yards left, that would be
yards left, that would be 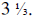
Now she cuts another strip of 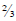 yards, leaving
yards, leaving
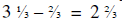 yards left. She cuts a third
yards left. She cuts a third
strip; that leaves 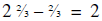 yards left, exactly. Now
wait a minute...she cut 3 strips and that
yards left, exactly. Now
wait a minute...she cut 3 strips and that
used up exactly half of what she started with. Okay, so if she cuts 6 strips she
will have used up
the whole thing.
Answer: 6.
What if we invert and multiply? 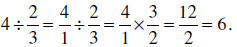
| Prev | Next |