Math 32 Discussion Problems
Polynomials
1. Use the quadratic formula (and factoring by grouping ) to
find all complex
solutions to the
given equations:
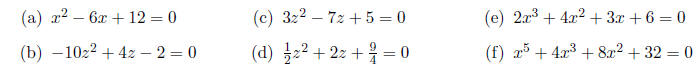
2. This problem explains one of the deep connections between complex numbers
and trigonometry .
You may have done it already, it was at the end of the handout from November 20.
Let's define a function from the real numbers to the complex numbers by the following formula:
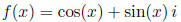
(a) Using and the sum -of-angles formula to show that f(x + y) = f(x) f(y).
(b) Use part (a) to show that f(3x) = f(x)3. More generally, show that f(nx) =
f(x)n for
any positive integer n.
(c) Expand out the formula in part (b) in terms of sines and cosines. I.e.
expand out
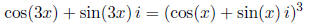
You should use the fact that (A + B)3 = A3 + 3A2B + 3AB2 + B3. What is i3?
(d) By comparing just the real parts or just the pure imaginary parts of your
answer to
problem (c), conclude formulas for cos(3x) and sin(3x).
(e) Use the fact that
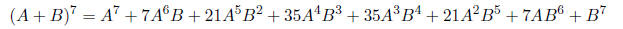
to derive formulas for cos(7x) and sin(7x).
3. Divide the following polynomials. Do these enough to get the hang of it
(maybe you already
have the hang of it from your homework.) Be sure to do the last four.
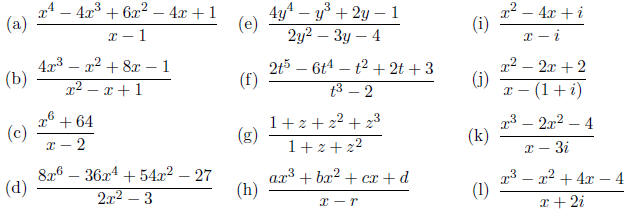
4. Find the value of k such that when x3 + kx + 1 is divided by x + 3, the remainder is -4.
5. For each of the following polynomials, I've listed one or more roots. Find
the rest of the roots.
(Hint: use synthetic division .)
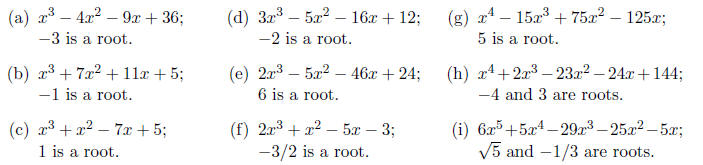
6. Find a polynomial of degree 3 . . .
(a) . . . such that the coefficient of x 3 is 1 and the roots are
3, -4, and 5.
(b) . . . with integer coefficients such that the roots are 1/2, 2/5, and -3/4.
(c) . . . with a root of multiplicity two at -1 and such that x + 6 is a factor.
7. Find all possible values of b such that one root of the equation x 2
+ bx + 1 = 0 is twice the
other one.
8. Let the roots of a polynomial be:
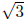 with
mulitplicity
with
mulitplicity
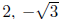 with
multiplicity 2, 4i with
with
multiplicity 2, 4i with
multiplicity 1, and -4i with multiplicity 1. If the leading coefficient is 1,
what is the polynomial?
9. Factor x4 + 64 into linear factors.
10. Define the nth quantum integer to be the polynomial
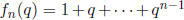 .
For example,
.
For example,
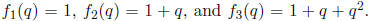 (The conventional notation is to write [n]
(The conventional notation is to write [n]
for fn, but I think this might be confusing.)
(a) What is fn(1)? What is fn(0)? What is fn(-1)?
What is fn(i)?
(b) What is fn(q)*f2(-q)?
(c) Use synthetic division to show that fn(q) is divisible by f2(q)
if and only if n is even.
(d) More generally, show that fn(q) is divisible by fd(q)
if and only if n is divisible by d.
(e) If d divides n, show that fn(q)=fd(q) = fn/d(qd).
(f) Completely factor 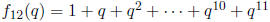
11. (a) Show that 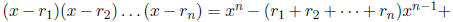 other terms, for
other terms, for
any integer n and numbers 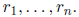
(b) Let r1, r2, r3, and r4
be four real roots of the equation 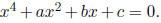 Show that
Show that
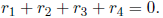 Hint: explain how to factor
Hint: explain how to factor
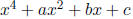 into linears .
into linears .
(c) Suppose that a circle intersects the parabola y = x^2
in the points (x1, y1), (x2, y2),
(x3, y3), and (x4, y4). Show that x1
+ x2 + x3 + x4 = 0.
| Prev | Next |