Multiplying and Dividing Rational Expressions
Examples of Rational expressions:
To Find the domain of a ration function, set the
DENOMINATOR equal to zero and
solve for x . These will be the only values NOT in your domain.
Examples: Find the values that aren 't in the domain. Then
write the domain in set
notation.
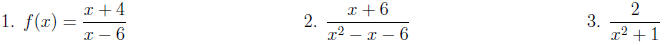
To get a rational expression in lowest terms, completely
factor the numerator and
denominator. Then cancel any common terms .
BE CAREFUL:
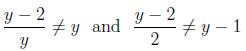
Examples: Write each rational expression in lowest terms.
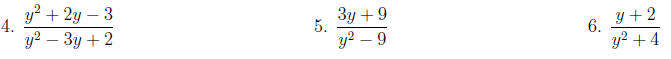
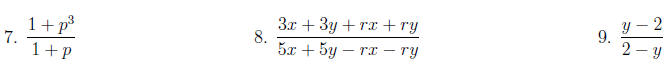
To multiply or divide rational expressions:
1. FACTOR everything completely.
2. If dividing, multiply by the reciprocal of the second term.
3. Cancel any terms that can be canceled .
4. Multiply across.
Examples:
Find the reciprocal:
Divide:
8.2 Adding and Subtracting Rational Expressions
To add or subtract rational expressions:
1. If the denominators are the same, add or subtract the
numerators and write that
over the common denominator.
2. If the denominators are different, first find the LCD.
Write each term with the
LCD as the denominator and then add or subtract.
3. SIMPLIFY.
Examples:
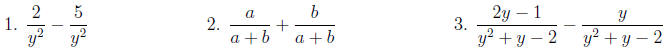
To find the LCD:
1. Completely factor each denominator.
2. Find the product of all the different factors taking the
greatest power from each
factor.
Find the LCD for the following denominators:
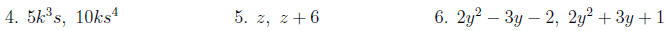
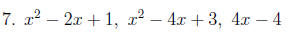
Adding and subtracting:
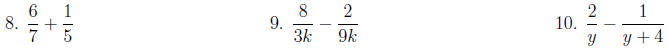
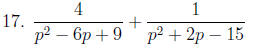
Examples of Complex Fractions:
Simplifying a Complex Fraction: Method 1.
1. Simplify the numerator and denominator separately.
2. Divide by multiplying the numerator by the reciprocal of the denominator.
3. Simplify, if possible.
Examples: Simplify.
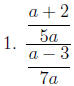
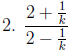
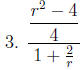
Method 2:
1. Multiply top and bottom by the LCD of the fractions.
2. Simplify.
Examples: Simplify.
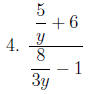
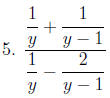
Now, pick your favorite method and simplify:
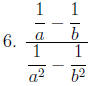
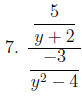
Simplify. Rid of all negative exponents.
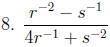
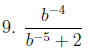
8.4 Equations with Rational Expressions and Graphs
Before we can solve rational equations, we need to make a
note of the DOMAIN of
any rational equation. This will be the intersection of the domains of each of
the
individual rational expressions.
Examples: Find the domain of each equation.
To solve a rational equation:
1. Find the domain of the equation.
2. Multiply both sides by the LCD to clear fractions.
3. Now, solve for x.
4. Eliminate any solutions that are NOT in the domain.
Solve:
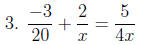
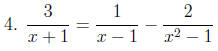
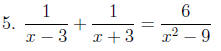
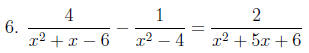
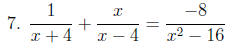
Graphing a rational function:
1. Find the values not in the domain. For each of these
values, draw a dotted vertical
line at y =that value. This is called a vertical asymptote.
2. If the degree of the denominator > degree of the
numerator, then draw a dotted
line at x = 0. This is called a horizontal asymptote.
3. Plot some points using an (x; y) chart. Then, connect
the dots in the "general"
rational function shape.
General rational function:
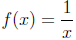
Examples:
1. Graph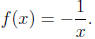 
2. Graph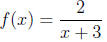 
8.5 Applications of Rational Expressions
Examples:
1. Suppose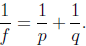 
Find p if f
= 15 and q = 25. Then find f if p = 6 and q = 9.
Remember when solving for a variable. You want that
variable to be on ONLY one
side of the equation.
2. Solve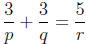 
for q.
3. Solve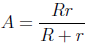 
for R.
Word Problems
40. p. 462 Suppose the following triangles are similar.
Find y and the lengths of the
two longest sides of each triangle.
6. p. 455 A plane travels 100 mi against the wind in the
same time it takes to travel
120 mi with the wind. The wind speed is 20 mph. Find the speed of the plane in
still
air.
7. p. 456 Dona Kenly drove 300 mi north from San Antonio,
mostly on the freeway.
She usually average 55 mph, but an accident slowed her speed through Dallas to
15
mph. If her trip took 6 hr, how many miles did she drive at reduced speed ?
8. p.457 a) Stan needs 45 min to do the dishes, while Deb
can do them in 30 min.
How long will it take them if they work together?
b) Suppose it takes Stan 35 min to do the dishes, and
together they can do them in
15 min. How long will it take Deb to do them alone?
| Prev | Next |