MATH 360 Review of Set Theory
Definition: A set is a collection of objects. The
objects that make up a set are
called its elements. Capital letters are used for sets, and lowercase for
elements. If
A is a set, then
• x ∈ A means x is an element of A.
• x 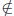 A means x is not an element of A.
A means x is not an element of A.
Example: Let A = {−1, 0, 2,Rebeccala}. Then −1 ∈ A, 3 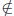 A, Rebeccala ∈ A.
A, Rebeccala ∈ A.
Recall the following important sets:
• Z = the integers = {0,±1,±2, ...}
• 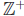 = the positive integers ={1, 2, 3, 4, ...}
= the positive integers ={1, 2, 3, 4, ...}
• N = the natural numbers = 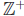
• Q = the rationals = {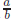 : a, b ∈ Z, b
≠ 0}
: a, b ∈ Z, b
≠ 0}
• P = the irrationals = numbers that cannot be expressed as a rational
• R = the real numbers = {x : x ∈ Q or x ∈ P}
• R+ = the positive real numbers = {x ∈ R : x > 0}
• Also, recall interval notation:
– (a, b) = {x ∈ R : a < x < b}
– [a, b] = {x ∈ R : a ≤ x ≤ b}
– (a,∞) = {x ∈ R : x > a} etc. Note that
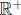 = (0,∞)
= (0,∞)
Interval notation should be quite familiar to you from your Calculus courses,
but if it is not, please come to see me - we'll go over it!
• The empty set, 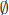 , is the set containing no elements. Sometimes
, is the set containing no elements. Sometimes 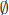 is written as
is written as
{ }. Note: {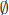 } ≠
} ≠ 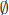 !
!
Definition: Let A and B be sets. Then A is a subset of B, written A 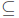 B, if
every
B, if
every
element of A is also an element of B. Formally, this means that if x ∈ A, then x
∈ B.
Thus, to have A 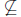 B means that there is at least one element of A that is not
also
B means that there is at least one element of A that is not
also
in B, i.e. there exists x ∈ A such that x 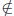 B.
B.
Example: A = {1, 2, 3, 4},B = {2, 4},C = {1, 3, 4}. Then B
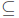 A and C
A and C 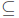 A, but
A, but
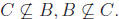
Definition: Two sets A and B are equal, written A = B, provided that A 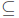 B and
B and
B 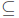 A.
A.
Definition: The union of two sets A and B is A ∪ B = {x : x ∈ A or x ∈ B}. The
intersection of two sets A and B is A ∩ B = {x : x ∈ A and x ∈ B}.
Example: Let A = (0, 3],B = [3,∞),C = {0, 6,Rebeccala}. Then A ∪ B =
(0,∞),A ∩ B = {3},A ∩ C = 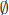 .
.
Definition: The sets A and B are disjoint if A ∩ B = 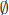 . Thus the sets A and C of
. Thus the sets A and C of
the example above are disjoint.
Definition: The set difference of A and B, A−B = {x : x ∈ A and x 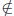 B}. Note:
B}. Note:
B does not have to be a subset of A in order to form A − B. This is sometimes
also
written as A\B.
Example: Let A = [0, 4],B = (1, 5],C = (3, 6),D = (1,∞). Then B − A =
(4, 5],A − B = [0, 1],C − D = 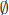 ,D − C = (1, 3] ∪ [6,∞).
,D − C = (1, 3] ∪ [6,∞).
Definition: The product (or Cartesian product) of sets A and B is the set A×B =
{(x, y) : x ∈ A and y ∈ B}. Note: the notation (x, y) here means the ordered
pair -
not the open interval. (Tricky! )
Examples:
1. If A = [1, 4],B = [2, 3], then A × B =
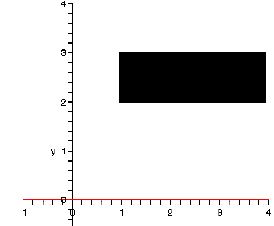
B × A =
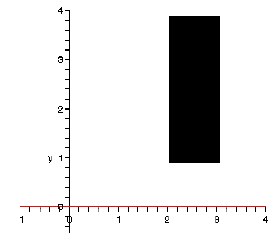
2. If A = {1, 2},B = {3, 4, 5}, then A×B = {(1, 3), (1,
4), (1, 5), (2, 3), (2, 4), (2, 5)}.
Thus if A and B are finite sets with m and n elements, respectively, then A×B
has mn elements. (This can be proven by induction.)
3. If A = [1, 3),B = [1, 2), then A × B =
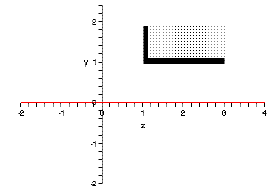
4. If A = (1,∞),B = (1, 2), then A × B =
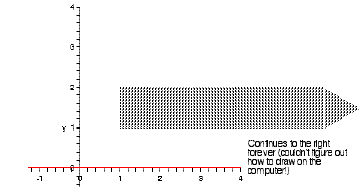
When drawing by hand , I use solid lines for the ”[” and
dotted lines for the ”(”
and arrows to indicate when it is continuing to infinity.
| Prev | Next |