Math ASSIGNMENT 9 SOLUTIONS
1. Let f . (a, b) -> R be continuous, with (a, b)
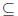 R. Show that if f(r) = 0 for each rational
R. Show that if f(r) = 0 for each rational
number r ∈(a, b), then f(x) = 0 for all x ∈(a, b).
Every real number x ∈(a, b) can be written as a limit of a sequence of
rational numbers,
{rn}. Thus, since f is continuous,
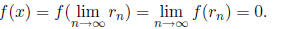
Thus, f(x) = 0 for all x ∈(a, b).
2. Let f . (a, b) -> R and g . (a, b) -> R be continuous, with (a, b) 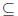 R, so
that f(r) = g(r) for
R, so
that f(r) = g(r) for
each rational number r ∈(a, b). Prove that f(x) = g(x) for all x ∈(a, b).
We will use the previous problem . We know that f(r) = g(r) for all rational
numbers in
(a, b). Thus, define h(x) = f(x)-g(x). Then, h is continuous and h(r) = 0 for
every rational
number in (a, b). Thus, h(x) = 0 for all x ∈(a, b). Therefore, f(x)-g(x) = 0 for
all x ∈(a, b)
and the conclusion follows.
3. Define the function f by
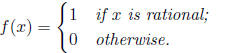
Show that f is discontinuous at every x ∈R.
We will show that it is discontinuous at each rational and at each
irrational. Note that each
rational number can be written as the limit of a sequence of rational numbers,
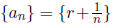
for n sufficiently large. Likewise , it can be written as the limit of a sequence
of irrational
numbers, 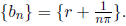 Thus, if f is continuous at r we
would have to have that
Thus, if f is continuous at r we
would have to have that
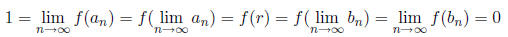
which cannot be, so f cannot be continuous at any rational number .
The similar argument will work to show that f is not continuous at any
irrational number.
4. Define the function h by
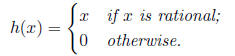
Show that h is continuous at x = 0 and at no other point.
Let {xn} be any sequence that converges to 0. Then given any
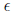 > 0 there is
an
> 0 there is
an 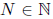 so
so
that if n > N then
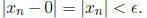 . When we apply h to this sequence, we get
a sequence
. When we apply h to this sequence, we get
a sequence
that is xn if xn is irrational and 0 if xn is rational. However, since {xn}
converges to 0, we
can show that for any 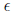 > 0 we can find an N
∈N so that if
> 0 we can find an N
∈N so that if 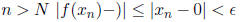
so the sequence 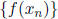 converges and f is continuous at x = 0.
converges and f is continuous at x = 0.
If x ≠ 0, then let
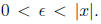 If x ∈Q then h(x) = 0, but there exists a
sequence of
If x ∈Q then h(x) = 0, but there exists a
sequence of
irrational numbers converging to x and the sequence
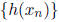 will also converge
to x but
will also converge
to x but
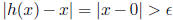 so that h cannot be continuous at x. If x ∈R\Q, there is a
sequence
so that h cannot be continuous at x. If x ∈R\Q, there is a
sequence
of rationals that converges to x but whose functional values are all 0. Again,
the function
does not take a sequence convergent to x to a sequence convergent to h(x), so it
cannot be
continuous at any x ∈R\Q.
5. For each rational number x, write x as p/q where p and q are integers with
no common factors
and q > 0. Define the function g by
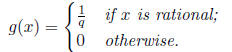
Thus, g(x) = 1 for all integers, 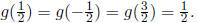 Show
that g is continuous at each
Show
that g is continuous at each
irrational and discontinuous at each rational.
First, note that for any x ∈R there is an n ∈Z and a ∈(0, 1) so that x = n +
a and
g(x) = g(n + a). If x is irrational, then so is a and we have that g(x) = g(a) =
0. If x is
rational, then so is a and g(x) = g(a). Thus, to understand g it suffices to look
at the values
of g for x ∈(0, 1).
Any irrational number, a, has a non-repeating decimal and we can consider
that decimal
expansion as one sequence converging to a. Given any 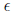 > 0 there is an
> 0 there is an 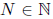 so
that
so
that
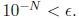 Thus, the sequence
Thus, the sequence
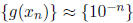 converges to 0.
converges to 0.
Now we need to show this for any sequence {xn} converging to a. Let 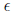 > 0 and
a ∈(0, 1)\Q.
> 0 and
a ∈(0, 1)\Q.
Let 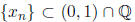 so that xn -> a. We can write
so that xn -> a. We can write
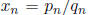 with
with 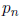 and
and
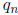 relatively
relatively
prime. We need to show that 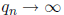 as n goes to infinity. If that is true, then
as n goes to infinity. If that is true, then
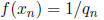
will go to 0 = f(a).
To show that 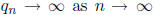 , we will assume not. Thus, there is an M ∈N so
that
, we will assume not. Thus, there is an M ∈N so
that
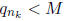 for k = 1, 2, 3, . . . . This means then that there are only a finite
number of fractions
for k = 1, 2, 3, . . . . This means then that there are only a finite
number of fractions
of the form
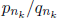 in (0, 1) with
in (0, 1) with
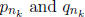 relatively prime. This means then
that the set
relatively prime. This means then
that the set
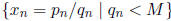 is finite. Thus, the limit of this sequence is a member of
the sequence,
is finite. Thus, the limit of this sequence is a member of
the sequence,
i.e., a = p/q so that q < M. Thus, a ∈Q. This is a contradiction. Thus, the
denominators
of the fractions must go to infinity and for any sequence {xn} converging to an
irrational a,
the sequence
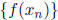 converges to 0 = f(a) and the function is continuous at a.
converges to 0 = f(a) and the function is continuous at a.
If r ∈Q and r = p/q , then g(r) = 1/q. Choose
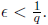 Now, for any sequence converging to r
Now, for any sequence converging to r
that contains irrational numbers
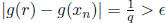 so there is no way to guarantee that
so there is no way to guarantee that
for all n sufficiently large the values of g are close to g(r). Thus, g is not
continuous at r.
6. Let f and g be continuous functions on [a, b] such that f(a) ≥ g(a) and
f(b) ≤ g(b). Prove
that
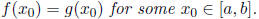
Define a function h(x) = g(x) - f(x) on [a, b]. Then note that h is continuous
and h(a) =
g(a) - f(a) ≤ 0 and h(b) = g(b) - f(b) ≥ 0. If h(a) = 0, then f(a) = g(a) and we
are done.
Likewise , if h(b) = 0 then f(b) = g(b) and we are done. Thus, assume that h(a)
≠ 0 (so
h(a) < 0) and assume that h(b) ≠ 0 (so h(b) > 0). Therefore, by the
Intermediate Value
Theorem, there is an x0 ∈(a, b) so that h(x0) = 0 and this implies that f(x0) =
g(x0).
7. Prove that 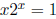 for some x ∈(0, 1).
for some x ∈(0, 1).
Define a function f on the interval [0, 1] by f(x) =
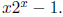 Then note that f
is continuous
Then note that f
is continuous
and f(0) = -1 < 0 and f(1) = 1 > 0. Therefore, by the Intermediate Value
Theorem , there
is an x ∈(0, 1) so that f(x) = 0. At that point we have
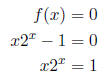
for some x ∈(0, 1).
| Prev | Next |